题目内容
10.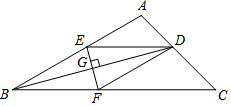 如图,在△ABC中,BD平分∠ABC交AC于D,EF垂直平分BD,分别交AB,BC,BD于E,F,G,连接DE,DF.
如图,在△ABC中,BD平分∠ABC交AC于D,EF垂直平分BD,分别交AB,BC,BD于E,F,G,连接DE,DF.(1)求证:DE=DF;
(2)若∠ABC=30°,∠C=45°,DE=4,求CF的长.
分析 (1)只要证明四边形BFDE是菱形即可;
(2)在Rt△DFH中,求出DH、FH,在Rt△DHC中,求出CH即可解决问题;
解答 (1)证明:∵EF垂直平分BD,
∴EB=ED,FB=FD.
∵BD平分∠ABC交AC于D,
∴∠ABD=∠CBD.
∵∠ABD+∠BEG=90°,∠CBD+∠BFG=90°,
∴∠BEG=∠BFG.
∴BE=BF.
∴四边形BFDE是菱形.
∴DE=DF.
(2)解:过D作DH⊥CF于H.
∵四边形BFDE是菱形,
∴DF∥AB,DE=DF=4.
在Rt△DFH中,∠DFC=∠ABC=30°,
∴DH=2,FH=$\sqrt{3}$DH=2$\sqrt{3}$,
在Rt△CDH中,∠C=45°,
∴DH=HC=2,
∴CF=CH+FH=2+2$\sqrt{3}$.
点评 本题考查菱形的性质,解直角三角形,直角三角形的30度角性质、等腰直角三角形的性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.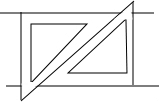 如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的依据是( )
如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的依据是( )
 如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的依据是( )
如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的依据是( )| A. | 同位角相等,两直线平行 | B. | 内错角相等,两直线平行 | ||
| C. | 同旁内角互补,两直线平行 | D. | 平行于同一条直线的两直线平行 |
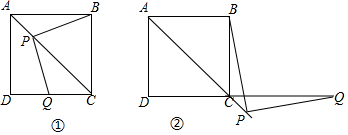
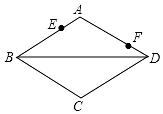 如图,周长为16的菱形ABCD中,点E,F分别在AB,AD边上,AE=1,AF=3,P为BD上一动点,则线段EP+FP的长最短为4.
如图,周长为16的菱形ABCD中,点E,F分别在AB,AD边上,AE=1,AF=3,P为BD上一动点,则线段EP+FP的长最短为4.
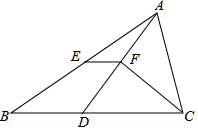 如图.在△ABC中,BC>AC,点D在BC上,且CD=AC,∠ACB的平分线CF交AD于点F,点E是AB的中点,连接EF.
如图.在△ABC中,BC>AC,点D在BC上,且CD=AC,∠ACB的平分线CF交AD于点F,点E是AB的中点,连接EF.