题目内容
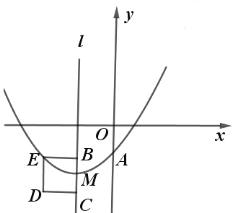
【题目】如图,已知抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 两点,点
两点,点![]() 坐标为
坐标为![]() ,抛物线的对称轴是直线
,抛物线的对称轴是直线![]()
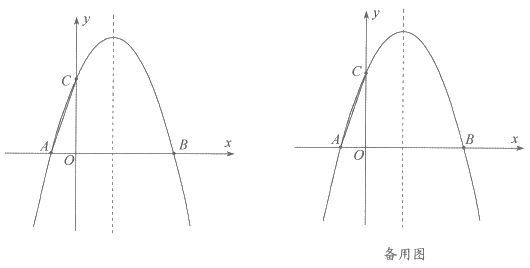
(1)求抛物线的解析式;
(2)点![]() 是
是![]() 轴右侧抛物线图像上的一动点,设点
轴右侧抛物线图像上的一动点,设点![]() 的横坐标为
的横坐标为![]() .
.
①是否存在这样的点![]() 使得
使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
②若该动点![]() 在第一象限内,连接
在第一象限内,连接![]() ,当
,当![]() 时,求
时,求![]() 的值
的值
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
![]()
【解析】
(1)将点A的坐标代入可得![]() ,由对称轴
,由对称轴![]() 得
得![]() ,联立可得
,联立可得![]() 的值,即可确定抛物线解析式;
的值,即可确定抛物线解析式;
(2)由点A、B、C坐标可知![]() .
.
① 分点P在第一象限和第四象限两种情况讨论,当点![]() 在第一象限时,过
在第一象限时,过![]() 作
作![]() 交
交![]() 延长线于
延长线于![]() ,作
,作![]() 轴于
轴于![]() ,易证
,易证![]() ,由
,由![]() 可知其相似比为
可知其相似比为![]() ,易知
,易知![]() 长,可得点
长,可得点![]() 坐标,求出直线
坐标,求出直线![]() 的解析式与抛物线解析式联立即可确定点P坐标;当
的解析式与抛物线解析式联立即可确定点P坐标;当![]() 在第四象限时,作
在第四象限时,作![]() 关于点
关于点![]() 的对称点,可知点P在直线
的对称点,可知点P在直线![]() 上,求出直线
上,求出直线![]() 的解析式与抛物线解析式联立即可确定点P坐标;
的解析式与抛物线解析式联立即可确定点P坐标;
②分别过![]() 作直线
作直线![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,并过
,并过![]() 作
作![]() 轴平行线交直线
轴平行线交直线![]() 于点
于点![]() 并设
并设![]() 轴交直线
轴交直线![]() 于点
于点![]() ,易得
,易得![]() ,于是
,于是![]() ,设直线
,设直线![]() 解析式为
解析式为![]() ,利用
,利用![]() 确定k值,求出直线
确定k值,求出直线![]() 解析式与抛物线解析式联立可得点P坐标,易知t值.
解析式与抛物线解析式联立可得点P坐标,易知t值.
解:(1)将点![]() 代入
代入![]() 得
得![]() ,由抛物线对称轴
,由抛物线对称轴![]() 得
得![]() ,联立得
,联立得![]() ,解得
,解得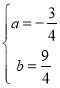 ,所以抛物线的解析式为
,所以抛物线的解析式为![]() ;
;
![]() 由
由![]() 得
得![]() ,
,![]()
![]() ,即
,即![]() .
.
①当![]() 在第一象限时,过
在第一象限时,过![]() 作
作![]() 交
交![]() 延长线于
延长线于![]() ,作
,作![]() 轴于
轴于![]()
![]() ,
,![]() ,
,![]() 轴
轴
![]()
![]()
![]()
![]() ,
,
其中![]() ,即相似比为
,即相似比为![]()
![]()
![]()
![]()
![]()
![]()
![]()
设直线![]() 解析式为
解析式为![]() ,
,
将点![]() ,
,![]() 代入
代入![]() 得
得
 ,解得
,解得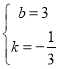
所以直线![]() 解析式为:
解析式为:![]()
联立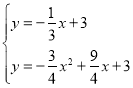
解得![]()
当![]() 在第四象限时,作
在第四象限时,作![]() 关于点
关于点![]() 的对称点
的对称点![]() ,则
,则![]() 在直线
在直线![]() 上.
上.
设直线![]() 解析式为
解析式为![]() ,
,
将点![]() 代入得
代入得![]() ,解得
,解得![]()
所以直线![]() 解析式为
解析式为![]()
联立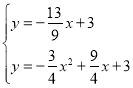
解得![]()
综上,![]() 点坐标为
点坐标为![]() 或
或![]()
即![]() 或
或![]() ;
;
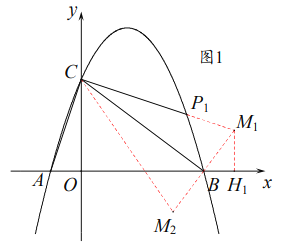
②如图,分别过![]() 作直线
作直线![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,并过
,并过![]() 作
作![]() 轴平行线交直线
轴平行线交直线![]() 于点
于点![]() 并设
并设![]() 轴交直线
轴交直线![]() 于点
于点![]() .
.
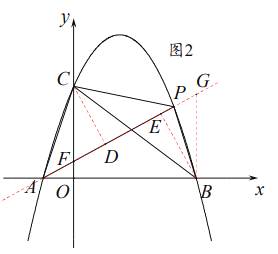
由作图可知![]() 轴,
轴,
![]()
![]() ,
,
![]()
设直线![]() 解析式为
解析式为![]() ,
,
则![]() .
.
由已知得![]()
解得![]()
联立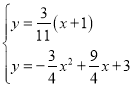
解得![]()
即![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某年级共有150名女生,为了解该校女生实心球成绩(单位:米)和仰卧起坐(单位:个)的情况,从中随机抽取30名女生进行测试,获得了她们的相关成绩,并对数据进行整理、描述和分析,下面给出了部分信息.
![]() .实心球成绩的频数分布表如下:
.实心球成绩的频数分布表如下:
分组 | 6.2≤ | 6.6≤ | 7.0≤ | 7.4≤ | 7.8≤ | 8.2≤ |
频数 | 2 |
| 10 | 6 | 2 | 1 |
![]() .实心球成绩在7.0≤
.实心球成绩在7.0≤![]() <7.4.这组的是:
<7.4.这组的是:
7.0 | 7.0 | 7.0 | 7.1 7.1 | 7.1 | 7.2 | 7.2 | 7.3 | 7.3 |
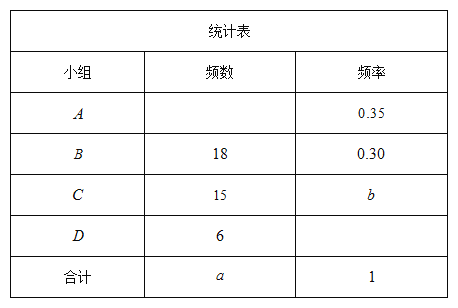
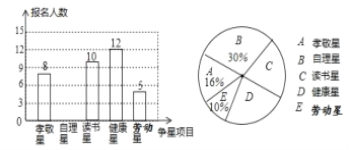
![]() .一分钟仰卧起坐成绩如图所示:
.一分钟仰卧起坐成绩如图所示:

根据以上信息,回答下列问题:
(1)①表中m的值为 ;
②抽取学生一分钟仰卧起坐成绩的中位数为 个;
(2)若实心球成绩达到7.2米及以上,成绩记为优秀,请估计全年级女生成绩达到优秀的人数.
(3)该年级某班体育委员将本班在这次抽样测试中被抽取的8名女生的两项成绩的数据抄录如下:
女生代码 | A | B | C | D | E | F | G | H |
实心球 | 8.1 | 7.7 | 7.5 | 7.5 | 7.3 | 7.2 | 7.0 | 6.5 |
一分钟仰卧起坐 | * | 42 | 47 | * | 47 | 52 | * | 49 |
其中有2名女生的一分钟仰卧起坐成绩未抄录完整,当老师说这8名女生恰好有4人两项测试成绩都达到了优秀,于是体育委员推测女生E的一分钟仰卧起坐成绩达到了优秀,你同意体育委员的说法吗?并说明你的理由.