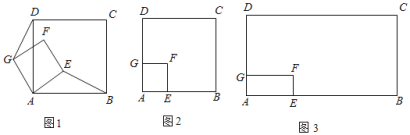
题目内容
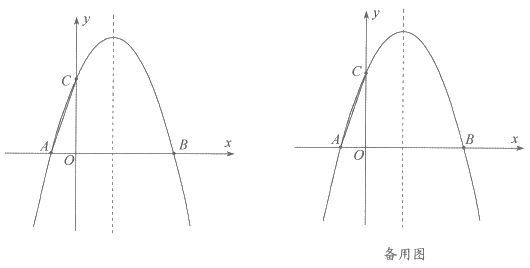
【题目】如图,抛物线![]()
![]() 过点
过点![]() ,顶点
,顶点![]() 在第三象限,
在第三象限,![]() ,
,![]() 是抛物线的对称轴
是抛物线的对称轴![]() 上的两点,且
上的两点,且![]() ,在直线
,在直线![]() 左侧以
左侧以![]() 为边作正方形
为边作正方形![]() ,点
,点![]() 恰好在抛物线上.
恰好在抛物线上.
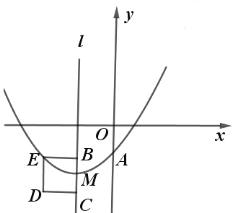
(1)用含![]() 的式子表示
的式子表示![]() ;
;
(2)求证:点![]() 和点
和点![]() 关于直线
关于直线![]() 对称;
对称;
(3)判断直线![]() 和直线
和直线![]() (
(![]() 是常数,且
是常数,且![]() )的交点是否在抛物线上,并说明理由.
)的交点是否在抛物线上,并说明理由.
【答案】(1)![]() ;(2)见解析;(3)直线
;(2)见解析;(3)直线![]() 和直线
和直线![]() 的交点
的交点![]() 不在抛物线上,理由见解析
不在抛物线上,理由见解析
【解析】
(1)把点a代入解析式中可得出结果;
(2)根据题意得出E点的坐标![]() ,代入解析式可得到F坐标,与B对比即可得到结果.
,代入解析式可得到F坐标,与B对比即可得到结果.
(3)根据条件求出CE所在直线的解析式,再根据![]() 得到
得到![]() ,可解的
,可解的![]() ,即可得到结果.
,即可得到结果.
(1)把![]() 代入
代入![]() ,得
,得![]() ,
,
即![]() ,
,
![]() ,
,
![]() .
.
(2)解:点![]() 在第三象限时,
在第三象限时,![]() ,设正方形
,设正方形![]() 的边长为
的边长为![]() ,则
,则![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
代入![]() ,得:
,得:
![]() ,解得:
,解得:![]()
![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() 与点
与点![]() 关于直线
关于直线![]() 对称.
对称.
(3)直线![]() 和直线
和直线![]() 的交点
的交点![]() 不在抛物线上.
不在抛物线上.
理由:由(2)得,点![]() ,点
,点![]() ,
,
设直线![]() 的解析式
的解析式![]() ,则有:
,则有:
![]() ,解得:
,解得:![]() ,
,
由![]() ,解得
,解得![]() ,
,
当![]() 时,
时,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() 直线
直线![]() 和直线
和直线![]()
![]() 的交点
的交点![]() 不在抛物线上.
不在抛物线上.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目