题目内容
在正方形ABCD中，点E、F分别在边AB、CD上，且AE=
AB，DF=
DC，DE与AF相交于点G，GH⊥AB，垂足为H．试用m、n的代数式表示
的值．
| 1 |
| m |
| 1 |
| n |
| AH |
| AB |
考点：正方形的性质,相似三角形的判定与性质
专题：
分析：延长HG交DC于点M，作FN∥HG交AB于点N，由△GAE∽△GFM，得出
=
，由△GHE∽△GHD，得出
=
，易得
=
，运用比例线段的性质得到
=
，即可得到
=
，根据
=
即可得出
=
．
| DF |
| AE |
| DG |
| EG |
| DG |
| EG |
| MG |
| HG |
| DF |
| AE |
| MG |
| HG |
| DF+AE |
| AE |
| MG+HG |
| HG |
| HG |
| NF |
| n |
| m+n |
| AH |
| AN |
| HG |
| NF |
| AH |
| AB |
| 1 |
| m+n |
解答：解：如图，延长HG交DC于点M，作FN∥HG交AB于点N，
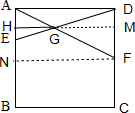
∵四边形ABCD是正方形，
∴AB∥DC，
∴△GAE∽△GFM，
∴
=
，
∵GH⊥AB，
∴△GHE∽△GHD，
∴
=
，
∴
=
，
∴
=
，即
=
，
∵AB=DC=BC=HM，
∴
=
，
∴
=
，
∵FN∥HG，
∴
=
，
∵AN=DF=
DC=
AB，
∴
=
，
∴
=
．
∵四边形ABCD是正方形，
∴AB∥DC，
∴△GAE∽△GFM，
∴
| DF |
| AE |
| DG |
| EG |
∵GH⊥AB，
∴△GHE∽△GHD，
∴
| DG |
| EG |
| MG |
| HG |
∴
| DF |
| AE |
| MG |
| HG |
∴
| DF+AE |
| AE |
| MG+HG |
| HG |
| ||||
|
| BC |
| HG |
∵AB=DC=BC=HM，
∴
| m+n |
| n |
| NF |
| HG |
∴
| HG |
| NF |
| n |
| m+n |
∵FN∥HG，
∴
| AH |
| AN |
| HG |
| NF |
∵AN=DF=
| 1 |
| n |
| 1 |
| n |
∴
| AH | ||
|
| n |
| m+n |
∴
| AH |
| AB |
| 1 |
| m+n |
点评：本题主要考查了正方形的性质及相似三角形的判定与性质，解题的关键是合理作出辅助线，运用三角形相似找出线段之间的关系．
练习册系列答案
阅读快车系列答案
相关题目
将6-（+3）-（-7）+（-2）中减法改成加法，写成省略加号和的形式且结果正确的（ ）
| A、-6-3+7-2=-4 |
| B、6-3-7-2=-6 |
| C、6-3+7-2=8 |
| D、6+3-7-2=0 |
已知圆锥的底面半径为r=2cm，高h=2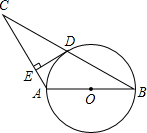
如图，△ABC中，AB=AC，以AB为直径的⊙O交BC于点D．
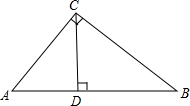如图，在Rt△ABC中，∠C=90°，CD⊥AB于D，设∠ACD=α，∠BCD=β，AC=8，BC=6，分别求cosα和tanβ的值．