Question

已知：如图，在△ABC中，∠C=90°，AC=BC=4，点M是边AC上一动点（与点A、C不重合），点N在边CB的延长线上，且AM=BN，连接MN交边AB于点P．

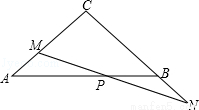
（1）求证：MP=NP；

（2）若设AM=x，BP=y，求y与x之间的函数关系式，并写出它的定义域；

（3）当△BPN是等腰三角形时，求AM的长．

Answer 1

（1）见解析

（2）y与x之间的函数关系式为，它的定义域是0＜x＜4

（3）

【解析】

试题分析：（1）过点M作MD∥BC交AB于点D，求出DM=BN，证△MDP≌△NBP即可；

（2）求出AB，根据△MDP≌△NBP推出DP=BP，推出方程即可；

（3）求出BP=BN，所得方程的解即可．

（1）证明：过点M作MD∥BC交AB于点D，

∵MD∥BC，

∴∠MDP=∠NBP，

∵AC=BC，∠C=90°，

∴∠A=∠ABC=45°，

∵MD∥BC，

∴∠ADM=∠ABC=45°，

∴∠ADM=∠A，

∴AM=DM．

∵AM=BN，

∴BN=DM，

在△MDP和△NBP中

，

∴△MDP≌△NBP，

∴MP=NP．

（2）【解析】
在Rt△ABC中，

∵∠C=90°，AC=BC=4，

∴．

∵MD∥BC，

∴∠AMD=∠C=90°．

在Rt△ADM中，AM=DM=x，

∴．

∵△MDP≌△NBP，

∴DP=BP=y，

∵AD+DP+PB=AB，

∴，

∴所求的函数解析式为，

定义域为0＜x＜4．

答：y与x之间的函数关系式为，它的定义域是0＜x＜4．

（3）【解析】
∵△MDP≌△NBP，

∴BN=MD=x．

∵∠ABC+∠PBN=180°，∠ABC=45°，

∴∠PBN=135°．

∴当△BPN是等腰三角形时，只有BP=BN，即x=y．

∴，

解得，

∴当△BPN是等腰三角形时，AM的长为．

答：AM的长为．