题目内容
6．不等式组$\left\{\begin{array}{l}{\frac{1}{2}x≤2}\\{3x-1＞0}\end{array}\right.$的解集是$\frac{1}{3}$＜x≤4．．分析 首先解每个不等式，两个不等式的解集的公共部分就是不等式组的解集．
解答 解：$\left\{\begin{array}{l}{\frac{1}{2}x≤2…①}\\{3x-1＞0…②}\end{array}\right.$，
解①得：x≤4，
解②得：x＞$\frac{1}{3}$．
则不等式组的解集是：$\frac{1}{3}$＜x≤4．
故答案是：$\frac{1}{3}$＜x≤4．
点评 本题考查的是一元一次不等式组的解，解此类题目常常要结合数轴来判断．还可以观察不等式的解，若x＞较小的数、＜较大的数，那么解集为x介于两数之间．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
1．与-3的积为1的数是（ ）
| A． | 3 | B． | $\frac{1}{3}$ | C． | -$\frac{1}{3}$ | D． | -3 |
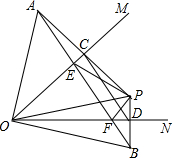如图，∠MON=45°，点P在∠MON内，OP=4，分别作点P关于OM、ON的对称点A、B，PA、PB分别交OM、ON于点C、D，连接AB分别交OM、ON于点E、F．
将一张长方形纸片折叠后如图，若∠2=45°，则∠1，∠3，∠4的度数是多少？