题目内容
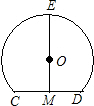
如图,M是CD的中点,EM⊥CD,若CD=4,EM=8,则![]() 所在圆的半径为
所在圆的半径为 ![]() .
.

考点:
垂径定理;勾股定理.
专题:
探究型.
分析:
首先连接OC,由M是CD的中点,EM⊥CD,可得EM过⊙O的圆心点O,然后设半径为x,由勾股定理即可求得:(8﹣x)2+22=x2,解此方程即可求得答案.
解答:
解:连接OC,
∵M是CD的中点,EM⊥CD,
∴EM过⊙O的圆心点O,
设半径为x,
∵CD=4,EM=8,
∴CM=CD=2,OM=8﹣OE=8﹣x,
在Rt△OEM中,OM2+CM2=OC2,
即(8﹣x)2+22=x2,
解得:x=![]() .
.
∴![]() 所在圆的半径为:
所在圆的半径为:![]() .
.
故答案为:![]() .
.

点评:
此题考查了垂径定理以及勾股定理.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
 如图,M是CD的中点,EM⊥CD,CD=2cm,EM=5cm,则
如图,M是CD的中点,EM⊥CD,CD=2cm,EM=5cm,则
 如图,M是CD的中点,EM⊥CD,若CD=4cm,EM=6cm,则弧CED所在圆的半径为
如图,M是CD的中点,EM⊥CD,若CD=4cm,EM=6cm,则弧CED所在圆的半径为 (2013•黄冈)如图,M是CD的中点,EM⊥CD,若CD=4,EM=8,则
(2013•黄冈)如图,M是CD的中点,EM⊥CD,若CD=4,EM=8,则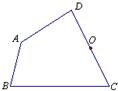 18、如图,O是CD的中点.以O为位似中心,用直尺和圆规作四边形ABCD的一个位似图形,使四边形ABCD的边长放大到原来的2倍.(保留作图痕迹,不必写出作法)
18、如图,O是CD的中点.以O为位似中心,用直尺和圆规作四边形ABCD的一个位似图形,使四边形ABCD的边长放大到原来的2倍.(保留作图痕迹,不必写出作法)