题目内容
如图，点D是△ABC边AB上的一点，BD=2AD，P是△ABC外接圆上一点（点P在劣弧 |
| AC |
| PB |
| PD |
考点：相似三角形的判定与性质,圆周角定理
专题：
分析：连接AP，由圆周角定理可得出∠APB=∠ACB，进而可得出∠APB=∠ACB=∠ADP，由相似三角形的判定定理可得出△APB∽△ADP，再根据相似三角形的对应边成比例即可得出结论．
解答：解：连接AP，
∵∠APB与∠ACB是
所对的圆周角，
∴∠APB=∠ACB，
∵∠ADP=∠ACB，
∴∠APB=∠ACB=∠ADP，
∵∠DAP=∠DAP，
∴△APB∽△ADP，
∴
=
=
，
∴AP2=AD•AB=AD•（AD+2AD）=3AD2，
∴
=
=
=
．
故答案为：
．
∵∠APB与∠ACB是
|
| AB |
∴∠APB=∠ACB，
∵∠ADP=∠ACB，
∴∠APB=∠ACB=∠ADP，
∵∠DAP=∠DAP，
∴△APB∽△ADP，
∴
| AP |
| AB |
| AD |
| AP |
| PD |
| PB |
∴AP2=AD•AB=AD•（AD+2AD）=3AD2，
∴
| PB |
| PD |
| AP |
| AD |
| ||
| AD |
| 3 |
故答案为：
| 3 |
点评：本题考查的是相似三角形的判定与性质及圆周角定理，根据题意作出辅助线，构造出相似三角形是解答此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
下列各组中的两项，属于同类项的有（ ）
①2x2y与-
x2y；②3a2bc与a2cb；③x3与x；④1与
；⑤m2n与mn2．
①2x2y与-
| 1 |
| 2 |
| 1 |
| 8 |
| A、2组 | B、3组 | C、4组 | D、5组 |
下列各式运算正确的是（ ）
| A、3x+3y=6xy |
| B、7x-5x=2x2 |
| C、16y2-7y2=9 |
| D、19a2b-9ba2=10a2b |
下列各式不属于分式的是（ ）
A、
| ||
B、-
| ||
C、
| ||
D、-
|
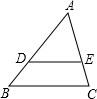如图，已知AD•AC=AE•AB，求证：DE∥BC．
如图，在△ABC中，已知∠BAC=90°，AD⊥BC于D，E是AB上一点，AF⊥CE于F，AD交CE于G点，