题目内容
1.写出图中3个三角形的面积S1、S2、S3之间的关系,并给出证明.
分析 设三个半圆的直径分别为:d1、d2、d3,半圆的面积=$\frac{1}{2}$π×($\frac{直径}{2}$)2,将d1、d2、d3代入分别求出S1、S2、S3,由勾股定理可得:d12+d22=d32,观察三者的关系即可,进而利用正方形以及等边三角形的性质分别求出各部分面积得出答案.
解答  解:如图①:设三个半圆的直径分别为:d1、d2、d3,
解:如图①:设三个半圆的直径分别为:d1、d2、d3,
S1=${\;}^{\frac{1}{2}}$×π×($\frac{{d}_{1}}{2}$)2=$\frac{{d}_{1}^{2}}{8}$π,
S2=$\frac{1}{2}$×π×($\frac{{d}_{2}}{2}$)2=$\frac{{d}_{2}^{2}}{8}$π,
S3=$\frac{1}{2}$×π×($\frac{{d}_{3}}{2}$)2=$\frac{{d}_{3}^{2}}{8}$π.
由勾股定理可得:
d12=d22+d32,
∴S3+S2=$\frac{π}{8}$(d32+d22)=$\frac{{d}_{1}^{2}}{8}$π=S1,
所以,S1、S2、S3的关系是:S3+S2=S1.
如图②:设AC=b,BC=a,AB=c,
则S2=a2,S3=b2,S1=c2,
又∵a2+b2=c2,
∴S1、S2、S3的关系是:S3+S2=S1.
如图③:设AC=b,BC=a,AB=c,
则S2=$\frac{1}{2}$×a×$\frac{\sqrt{3}}{2}$a=$\frac{\sqrt{3}}{4}$a2,S3=$\frac{1}{2}$×b×$\frac{\sqrt{3}}{2}$b=$\frac{\sqrt{3}}{4}$b2,
S1=$\frac{1}{2}$×c×$\frac{\sqrt{3}}{2}$c=$\frac{\sqrt{3}}{4}$c2,
又∵a2+b2=c2,
∴S1、S2、S3的关系是:S3+S2=S1.
点评 本题主要考查了运用勾股定理结合图形求面积之间的关系,关键在于根据题意找出直角三角形,运用勾股定理求出三个半圆的直径之间的关系.

 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案| A. |  | B. |  | C. |  | D. |  |
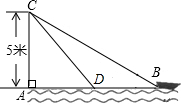 如图,在离水面高度为5米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13米,此人以0.5米每秒的速度收绳,10秒后船移动到点D的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号)
如图,在离水面高度为5米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13米,此人以0.5米每秒的速度收绳,10秒后船移动到点D的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号) | A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |