题目内容
16. 如图,在△ABC中,AB=3,AC=2.当∠B最大时,BC的长是( )
如图,在△ABC中,AB=3,AC=2.当∠B最大时,BC的长是( )| A. | 1 | B. | $\sqrt{5}$ | C. | $\sqrt{13}$ | D. | 5 |
分析 以AC为直径作⊙O,当BC为⊙O的切线时,即BC⊥AC时,∠B最大,根据勾股定理即可求出答案.
解答 解:以AC为直径作⊙O,当BC为⊙O的切线时,即BC⊥AC时,∠B最大,
此时BC=$\sqrt{A{B}^{2}{-AC}^{2}}$=$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$.
故选B.
点评 本题考查了切线的性质,勾股定理,利用切线的性质判断出BC为⊙O的切线时∠B最大是解题的关键.

练习册系列答案
相关题目
18.下列命题中,属于真命题的是( )
| A. | 三点确定一个圆 | B. | 圆内接四边形对角互余 | ||
| C. | 若a2=b2,则a=b | D. | 若$\root{3}{a}$=$\root{3}{b}$,则a=b |
7.为庆祝“六一”儿童节,某幼儿园举行用火柴棒摆金鱼的比赛,如图所示.

按以上的规律,第n个图形需要的火柴棒m关于n的函数表达式为( )

按以上的规律,第n个图形需要的火柴棒m关于n的函数表达式为( )
| A. | m=8n | B. | m=8+6n | C. | m=4+4n | D. | m=2+6n |
5.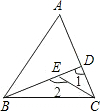 如图所示:D是△ABC中AC边上的一点,E是BD上一点,则对∠1,∠2,∠A之间的关系描述正确的是( )
如图所示:D是△ABC中AC边上的一点,E是BD上一点,则对∠1,∠2,∠A之间的关系描述正确的是( )
 如图所示:D是△ABC中AC边上的一点,E是BD上一点,则对∠1,∠2,∠A之间的关系描述正确的是( )
如图所示:D是△ABC中AC边上的一点,E是BD上一点,则对∠1,∠2,∠A之间的关系描述正确的是( )| A. | ∠A<∠1<∠2 | B. | ∠2<∠1<∠A | C. | ∠1>∠2>∠A | D. | 无法确定 |
6.若a=-0.32,b=-3-2,$c={({-\frac{1}{3}})^{-2}}$;$d={({-\frac{1}{3}})^0}$,则它们的大小关系是( )
| A. | a<b<c<d | B. | b<a<d<c | C. | a<d<c<b | D. | c<a<d<b |
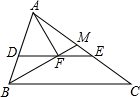 如图,已知△ABC中,∠ABC的平分线为BM,过A作AF⊥BM,垂足为F,过F作BC的平行线交AB于D,交AC于E,EF=2,AB=6,则BC=10.
如图,已知△ABC中,∠ABC的平分线为BM,过A作AF⊥BM,垂足为F,过F作BC的平行线交AB于D,交AC于E,EF=2,AB=6,则BC=10.