题目内容
4.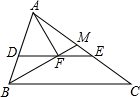 如图,已知△ABC中,∠ABC的平分线为BM,过A作AF⊥BM,垂足为F,过F作BC的平行线交AB于D,交AC于E,EF=2,AB=6,则BC=10.
如图,已知△ABC中,∠ABC的平分线为BM,过A作AF⊥BM,垂足为F,过F作BC的平行线交AB于D,交AC于E,EF=2,AB=6,则BC=10.
分析 延长AF交BC于G,根据等腰三角形的性质和判定得到AF=FG,BA=BG,得到EF是△ACG的中位线,求出CG,计算得到答案.
解答 解: 延长AF交BC于G,
延长AF交BC于G,
∵∠ABC的平分线为BM,过A作AF⊥BM,
∴AF=FG,BA=BG,
又EF∥CG,
∴EF=$\frac{1}{2}$CG,
∴CG=2EF=4,
BC=BG+GC=AB+GC=6+4=10,
故答案为:10.
点评 本题考查的是三角形的中位线定理和等腰三角形的判定和性质,正确作出辅助线得到三角形的中位线是解题的关键.

练习册系列答案
相关题目
7.射击训练中,甲、乙、丙、丁四人每人射击10次,平均环数均为8.7环,方差分别为S甲2=0.51,S乙2=0.41、S丙2=0.62、S丁2=0.45,则四人中成绩最稳定的是( )
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
16. 如图,在△ABC中,AB=3,AC=2.当∠B最大时,BC的长是( )
如图,在△ABC中,AB=3,AC=2.当∠B最大时,BC的长是( )
 如图,在△ABC中,AB=3,AC=2.当∠B最大时,BC的长是( )
如图,在△ABC中,AB=3,AC=2.当∠B最大时,BC的长是( )| A. | 1 | B. | $\sqrt{5}$ | C. | $\sqrt{13}$ | D. | 5 |
 已知甲、乙、丙三个村计划修建一个贮物库,使三个村到贮物库的距离一样,请你帮这三个村设计贮物库的具体位置.
已知甲、乙、丙三个村计划修建一个贮物库,使三个村到贮物库的距离一样,请你帮这三个村设计贮物库的具体位置.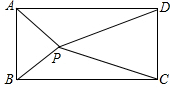 如图,四边形ABCD是长方形,点P是长方形内的任意一点,求证:PA2+PC2=PB2+PD2.
如图,四边形ABCD是长方形,点P是长方形内的任意一点,求证:PA2+PC2=PB2+PD2.