题目内容
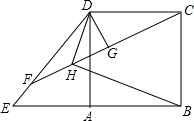 已知:如图,正方形ABCD中,点E是BA延长线上一点,连接DE,点F在DE上且DF=DC,DG⊥CF于G.DH平分∠ADE交CF于点H,连接BH.
已知:如图,正方形ABCD中,点E是BA延长线上一点,连接DE,点F在DE上且DF=DC,DG⊥CF于G.DH平分∠ADE交CF于点H,连接BH.(1)若DG=2,求DH的长;
(2)求证:BH+DH=
| 2 |
考点:正方形的性质,全等三角形的判定与性质
专题:
分析:(1)通过证明△DGH是等腰直角三角形,得到DH=
DG=2
;
(2)如图,过点C作CM⊥CH,交HD延长线于点M.构建等腰直角△HCM和全等三角形△MCD≌△HCB,所以根据等腰直角三角形的性质和全等三角形的性质推知MH=
CH,DM=BH.则BH+DH=MH=
CH.
| 2 |
| 2 |
(2)如图,过点C作CM⊥CH,交HD延长线于点M.构建等腰直角△HCM和全等三角形△MCD≌△HCB,所以根据等腰直角三角形的性质和全等三角形的性质推知MH=
| 2 |
| 2 |
解答:
(1)解:∵如图,DF=DC,DG⊥CF,
∴∠FDG=
∠FDC.
∵DH平分∠ADE,
∴∠FDH=
∠ADF,
∴∠HDG=∠FDG-∠FDH=
(∠FDC-∠ADF)=
∠ADC=45°.
∴△DGH是等腰直角三角形,
∵DG=2,
∴DH=2
;
(2)证明:如图,过点C作CM⊥CH,交HD延长线于点M.
∵∠DCB=90°,
∴∠1=∠2(同角的余角相等).
又∵△DGH是等腰直角三角形,
∴△MCH是等腰直角三角形,
∴MC=CH.
∴MH=
CH.
∵在△MCD与△HCB中,
,
∴△MCD≌△HCB)SAS),
∴DM=BH.
∴BH+DH=DM+DH=MH=
CH.即BH+DH=
CH.

(1)解:∵如图,DF=DC,DG⊥CF,
∴∠FDG=
| 1 |
| 2 |
∵DH平分∠ADE,
∴∠FDH=
| 1 |
| 2 |
∴∠HDG=∠FDG-∠FDH=
| 1 |
| 2 |
| 1 |
| 2 |
∴△DGH是等腰直角三角形,
∵DG=2,
∴DH=2
| 2 |
(2)证明:如图,过点C作CM⊥CH,交HD延长线于点M.
∵∠DCB=90°,
∴∠1=∠2(同角的余角相等).
又∵△DGH是等腰直角三角形,
∴△MCH是等腰直角三角形,
∴MC=CH.
∴MH=
| 2 |
∵在△MCD与△HCB中,
|
∴△MCD≌△HCB)SAS),
∴DM=BH.
∴BH+DH=DM+DH=MH=
| 2 |
| 2 |
点评:本题考查了全等三角形的判定与性质,正方形的性质.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
我国自主研发的通用计算机CPU芯片已经达到“奔腾Ⅲ”水平,由中科院计算所研制的高性能通用处理器“龙芯”二号,单精度峰值浮点运算速度为20亿次/秒,这个数字用科学记数法可表示为( )
| A、20×108 |
| B、2×108 |
| C、2×109 |
| D、20×109 |
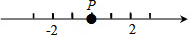 某校为培育青少年科技创新能力,举办了动漫制作活动,小明设计了点P在数轴上做直线运动的一个雏形,如图所示.点P从原点开始运动至停止的记录为:+12,-8,-2,-7,+3.问:当运动停止时,点P位置上的数是多少?
某校为培育青少年科技创新能力,举办了动漫制作活动,小明设计了点P在数轴上做直线运动的一个雏形,如图所示.点P从原点开始运动至停止的记录为:+12,-8,-2,-7,+3.问:当运动停止时,点P位置上的数是多少?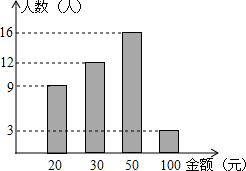 2010年全国多个省市遭受严重干旱.重庆市某中学九年级(一)班共40名同学开展了“我为旱区献爱心”的活动,活动结束后,生活委员小林将捐款情况进行了统计,并绘制成统计图如下.
2010年全国多个省市遭受严重干旱.重庆市某中学九年级(一)班共40名同学开展了“我为旱区献爱心”的活动,活动结束后,生活委员小林将捐款情况进行了统计,并绘制成统计图如下. 如图,点A、B分别在二次函数y=x2的图象上,且线段AB⊥y轴,若AB=6,试求点A、B的坐标.
如图,点A、B分别在二次函数y=x2的图象上,且线段AB⊥y轴,若AB=6,试求点A、B的坐标. 如图,已知平行四边形ABCD中,点E、F分别是DC、AB的中点,AE、CF与对角线BD分别交于点G、H.
如图,已知平行四边形ABCD中,点E、F分别是DC、AB的中点,AE、CF与对角线BD分别交于点G、H.