题目内容
1.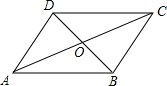 在2013年“植树月“的活动中,某校为了绿化校园,决定修建一个平行四边形花园(如图所示,图中的线段代表小路).已知D0=BO=5m,AC=26m,∠ADB=90°,求小路BC的长和花园的面积.
在2013年“植树月“的活动中,某校为了绿化校园,决定修建一个平行四边形花园(如图所示,图中的线段代表小路).已知D0=BO=5m,AC=26m,∠ADB=90°,求小路BC的长和花园的面积.
分析 根据勾股定理求得AD的长,再根据对角线互相平分的四边形是平行四边形证明四边形ABCD是平行四边形,从而根据平行四边形的对边相等就可求得BC的长;根据平行四边形的面积公式可以求得它的面积.
解答 解:在△AOD中,∠ADB=90°,AC=26,0D=5,
根据勾股定理,得
AD2=OA2-OD2=132-52=144,
∴AD=12.
∵AC=26,AD=12,
∴OA=OC.
又DO=OB,
∴四边形ABCD为平行四边形.
∴AD=BC=12.
∵∠ADB=90°,
∴AD⊥BD.
∴S四边形ABCD=AD•BD=12×10=120.
答:BC的长为12,四边形ABCD的面积为120.
点评 此题综合运用了勾股定理、平行四边形的判定和性质,熟练掌握平行四边形的判定定理是解题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
16.对车间10名工人上月生产情况进行统计,结果如下所示(单位:件),则这10名工人上个月平均每人生产14.4件.
| 产量(件) | 40 | 30 | 10 | 8 |
| 人数(人) | 1 | 1 | 5 | 3 |
 如图,A、O、C在同一直线上,
如图,A、O、C在同一直线上,