题目内容
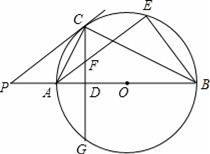
如图，在△ABC中
（1）作图，作BC边的垂直平分线分别交于AC，BC于点D，E（用尺规作图法，保留作图痕迹，不要求写作法）
（2）在（1）条件下，连接BD，若BD=9，BC=12，求∠C的余弦值．
【考点】作图—基本作图；线段垂直平分线的性质；解直角三角形．
【分析】（1）分别以B、C为圆心，大于BC的一半长为半径画弧，两弧交于两点，再过两点画直线即可；
（2）根据线段垂直平分线的性质可得EC=
BC=6，BD=CD=9，再根据余弦定义可得答案．
【解答】解：（1）如图所示：
（2）∵DE是BC的垂直平分线，
∴EC=BC=6，BD=CD=9，
∴cos∠C=
=
=
．
【点评】此题主要考查了基本作图，以及三角函数定义，关键是掌握线段垂直平分线的画法，以及线段垂直平分线上任意一点，到线段两端点的距离相等．
练习册系列答案
相关题目
点出发，沿东北方向航行至
点，再从
方向航行至
点，则
等于 。
（x＞0）的图象经过点A（2
，1），射线AB与反比例函数的图象交于另一点B（1，a），射线AC与y轴交于点C，∠BAC=75°，AD⊥y轴，垂足为D．
