题目内容
4．某旅行社有100张床位，每张床位收费10元，床位可全部租出，若每张床位的收费提高2元，则减少10张床位的租出，以每次提高2元的这种方式变化下去，为了获得1120元的收入，每张床位的收费每晚应提高多少元？分析 利用旅行社有100张床位，每床每晚收费10元，当提高2元，则减少10张床位租出，可得出每张床的租金与出租的床位数，两者的乘积即是所获得利润．
解答 解：设每张床位的收费每晚应提高x元，由题意得：
（100-$\frac{x}{2}$×10）（10+x）=1120，
解得：x1=4，x2=6．
答：每张床位收费每晚应提高4元或6元．
点评 此题主要考查了一元二次方程中的应用；根据题意列出方程是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
18．十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数（F）、棱数（E）之间存在的一个有趣的关系式，被称为欧拉公式请你观察下列几种简单多面体模型，解答下列问题：
（1）根据上面多面体的模型，完成表格中的空格：
你发现顶点数（V）、面数（F）、棱数（E）之间存在的关系式是V+F-E=2；
（2）一个多面体的棱数比顶点数大10，且有12个面，则这个多面体的棱数是30；
（3）某个玻璃饰品的外形是简单的多面体，它的外表面是由三角形和八边形两种多边形拼接而成，每个顶点处都有3条棱，共有棱36条．若该多面体外表面三角形的个数比八边形的个数的2倍多2，求该多面体外表面三角形的个数．
（1）根据上面多面体的模型，完成表格中的空格：
| 多面体 | 顶点数（V） | 面数（F） | 棱数（E） |
| 四面体 | 4 | 4 | 6 |
| 长方体 | 8 | 6 | 12 |
| 正八面体 | 6 | 8 | 12 |
（2）一个多面体的棱数比顶点数大10，且有12个面，则这个多面体的棱数是30；
（3）某个玻璃饰品的外形是简单的多面体，它的外表面是由三角形和八边形两种多边形拼接而成，每个顶点处都有3条棱，共有棱36条．若该多面体外表面三角形的个数比八边形的个数的2倍多2，求该多面体外表面三角形的个数．
如图，AB=16cm，延长AB到C，使BC=3AB，D是BC的中点，求AD的长度．
某供电公司，为了鼓励居民用电，采用分段计费的方法来计算电费，月用电x（度）与相应电费y（元）之间的函数的图象如图所示．
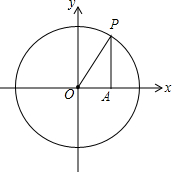如图，动点P沿着半径为1的单位圆绕原点旋转，线段OP在x轴的投影为OA．