题目内容
 如图,A、B是函数y=kx与函数y=
如图,A、B是函数y=kx与函数y=| 1 |
| x |
考点:反比例函数系数k的几何意义
专题:
分析:设A点坐标为(x、
),根据A、B两点关于原点对称可知,B点坐标为(-x,-
),可求出C点坐标,利用矩形的面积公式可求出矩形OECD的面积,再根据反比例函数中系数k的几何意义可求出△AOD与△BOE的面积,把矩形OECD的面积与两三角形的面积相加即可得出结论.
| 1 |
| x |
| 1 |
| x |
解答: 解:设BC与y轴交于点E,如图所示,
解:设BC与y轴交于点E,如图所示,
设A点坐标为(x、
),则B点坐标为(-x,-
),
∴C点坐标为(x,-
),
∴S矩形OECD=x•|-
|=1,
∵A、B为函数y=
图象上两点,
∴S△AOD=S△BOE=
k=
,
∴S△ABC=S矩形OECD+S△AOD+S△BOE=1+
+
=2.
 解:设BC与y轴交于点E,如图所示,
解:设BC与y轴交于点E,如图所示,设A点坐标为(x、
| 1 |
| x |
| 1 |
| x |
∴C点坐标为(x,-
| 1 |
| x |
∴S矩形OECD=x•|-
| 1 |
| x |
∵A、B为函数y=
| 1 |
| x |
∴S△AOD=S△BOE=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ABC=S矩形OECD+S△AOD+S△BOE=1+
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是反比例函数中系数k的几何意义,根据A、B两点关于原点对称求出C点坐标,进而求出四边形OECD的面积是解答此题的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
分式
有意义,则x的取值范围是( )
| 2x |
| x+1 |
| A、x≠1 | B、x≠0 |
| C、x=-1 | D、x≠-1 |
在同学们学习的运算法则中,我们补充定义新运算“%”,它的运算规则是:a%b=(a-b)×(b-a),则3%6=( )
| A、9 | B、18 | C、-9 | D、2 |
 如图有两个边长为4cm的正方形,其中一个正方形的顶点在另一个正方形的中心上,绕着中心旋转其中一个正方形,那么图中阴影部分的面积是( )
如图有两个边长为4cm的正方形,其中一个正方形的顶点在另一个正方形的中心上,绕着中心旋转其中一个正方形,那么图中阴影部分的面积是( )| A、无法确定 |
| B、8cm2 |
| C、16cm2 |
| D、4cm2 |
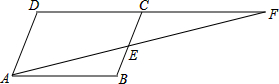 如图,?ABCD中,E为BC中点,连接AE交DC的延长线于F,求证:AE=EF.
如图,?ABCD中,E为BC中点,连接AE交DC的延长线于F,求证:AE=EF.