题目内容
4．求1+3+32+33+34+…+3n的值（其中n为正整数）．分析 设原式为M，将两边同时乘以3，得到3M，两式相减，再两边同时除以2即可．
解答 解：设M=1+3+32+33+…+3n①，
则3M=3+32+33+34…+3n+1②，
②-①，得：2M=3n+1-1，
两边同时除以2，得M=$\frac{{3}^{n+1}-1}{2}$．
点评 本题考查了有理数的乘方，理解求和的运算方法是解题的关键解决此类问题时，我们通常用将原式扩大倍数的方式解答．
练习册系列答案
相关题目
19．
如图．在平行四边形ABCD中，对角线AC，BD相交成的锐角为60°，若AC=8，BD=6．点E是BC的中点．则△ABE的面积是（ ）
如图．在平行四边形ABCD中，对角线AC，BD相交成的锐角为60°，若AC=8，BD=6．点E是BC的中点．则△ABE的面积是（ ）| A． | 24$\sqrt{3}$ | B． | 12$\sqrt{3}$ | C． | 6$\sqrt{3}$ | D． | 3$\sqrt{3}$ |
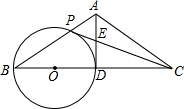已知：如图，在等腰△ABC中，AB=AC，点D是边BC的中点，以BD为直径作⊙O，交边AB于点P，连接PC交AD于点E，且AE=DE．