题目内容
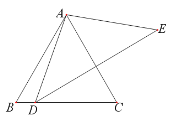
【题目】联想三角形外心的概念,我们可引入如下概念:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.例:已知![]() ,则点
,则点![]() 为
为![]() 的准外心(如图
的准外心(如图![]() ).
).
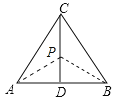
![]() 如图
如图![]() ,
,![]() 为正三角形
为正三角形![]() 的高,准外心
的高,准外心![]() 在高
在高![]() 上,且
上,且![]() ,求
,求![]() 的度数.
的度数.
![]() 如图
如图![]() ,若
,若![]() 为直角三角形,
为直角三角形,![]() ,
,![]() ,
,![]() ,准外心
,准外心![]() 在
在![]() 边上,试探究
边上,试探究![]() 的长.
的长.



【答案】∠APB=90°;(2)PA=![]() 或6.
或6.
【解析】
(1)利用分类讨论:①若PB=PC,②若PA=PC,③若PA=PB,进而求出即可;
(2)利用分类讨论:①若PB=PA,②若PA=PC,③若PC=PB,进而求出即可.
(1)①若PB=PC,连结PB,则∠PCB=∠PBC.
∵CD为等边三角形的高.∴AD=BD,∠PCB=30°,
∴∠PBD=∠PBC=30°,∴PD=![]() DB=
DB=![]() AB.
AB.
与已知PD=![]() AB矛盾,∴PB≠PC.
AB矛盾,∴PB≠PC.
②若PA=PC,连结PA,
则∠PCA=∠PAC.
∵CD为等边三角形的高.∴AD=BD,∠PCA=30°,
∴∠PAD=∠PAC=30°,∴PD=![]() DA=
DA=![]() AB.
AB.
与已知PD=![]() AB矛盾,∴PA≠PC.
AB矛盾,∴PA≠PC.
③若PA=PB,由PD=![]() AB,得PD=BD,
AB,得PD=BD,
∴∠BPD=45°,
故∠APB=90°;
(2)①若PB=PA,设PA=x,
∵∠C=90°,AB=13,BC=5,
∴AC=12,则CP=12-x,
∴x2=(12-x)2+52,
∴解得:x=![]() ,即PA=
,即PA=![]() .
.
②若PA=PC,则PA=6.
③若PC=PB,由图知,
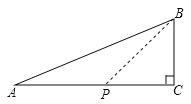
在Rt△PBC中,不可能,
故PA=![]() 或6.
或6.

练习册系列答案
相关题目