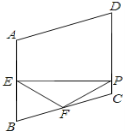
题目内容
【题目】如图,边长为![]() 的正方形
的正方形![]() 的对角线交于点
的对角线交于点![]() ,把边
,把边![]() 、
、![]() 分别绕点
分别绕点![]() 、
、![]() 同时逆时针旋转
同时逆时针旋转![]() 得四边形
得四边形![]() ,其对角线交点为
,其对角线交点为![]() ,连接
,连接![]() .下列结论:
.下列结论:
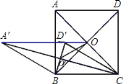
①四边形![]() 为菱形;
为菱形;
②![]() ;
;
③线段![]() 的长为
的长为![]() ;
;
④点![]() 运动到点
运动到点![]() 的路径是线段
的路径是线段![]() .其中正确的结论共有( )
.其中正确的结论共有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
①根据旋转角是60°以及正方形的四个角都是直角可得∠BCD′=30°,然后证明A′B∥CD′,进而得到四边形A′BCD′是平行四边形,再根据A′B=BC,即可证明四边形A′BCD′是菱形;
②根据旋转角是60°求出点B到A′D′的距离是A′B的一半,也就是AB的一半,然后根据正方形的面积公式以及菱形的面积即可证明;
③先求出OA′的长度,再根据菱形的对边相等,减去正方形的边长即可;
④根据旋转的性质,点O以BC的中点为圆心,以BC的一半为半径逆时针旋转可以得到点O′,所以路径是弧而非线段.
①根据题意,∠A′BA=∠D′CD=60°,
∵四边形ABCD是正方形,
∴∠BCD=90°,
∴∠BCD′=30°,
∴∠A′BC+∠BCD′=60°+90°+30°=180°,
∴A′B∥CD′,
又∵A′B=CD′=AB,
∴四边形A′BCD′是平行四边形,
∵AB=BC(正方形的边长相等),
∴四边形A′BCD′是菱形,故本题小题正确;
②∵∠ABA′=60°,AB=2,
∴点B到A′D′的距离是:![]() A′B=
A′B=![]() AB=1,
AB=1,
∴S四边形A′BCD=BC(![]() A′B)=2×1=2,
A′B)=2×1=2,
S正方形ABCD=BCAB=2×2=4,
∴S四边形A′BCD=![]() S正方形ABCD,故本小题正确;
S正方形ABCD,故本小题正确;
③∵点O是AC的中点,
∴OA′=A′Bsin60°+![]() BC=2×
BC=2×![]() +
+![]() ×2=
×2=![]() +1,
+1,
∴OD′=OA′A′D′=![]() +12=
+12=![]() 1,故本小题正确;
1,故本小题正确;
④根据菱形的对角线互相垂直可得△BCO′是直角三角形,
∴以BC的中点为圆心,以BC的一半为半径,点O逆时针旋转可以到达点O′的位置,经过路径是弧而不是线段OO′,故本小题错误.
综上所述,正确的结论有①②③共3个.
故选:C.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案