题目内容
13.在一个不透明的口袋里装有四个小球,球面上分别标有数字-2、0、1、2,它们除数字不同外没有任何区别,每次实验先搅拌均匀.(1)从中任取一球,求抽取的数字为负数的概率;
(2)从中任取一球,将球上的数字记为x(不放回);再任取一球,将球上的数字记为y,试用画树状图(或列表法)表示所有可能出现的结果,并求“x+y>0”的概率.
分析 (1)直接根据概率公式求解即可;
(2)先利用树状图展示12种等可能的结果数,再得到x+y>0的所有可能的数目,即可求出其概率.
解答 解:(1)根据题意得:抽取的数字为负的情况有1个,则P(数字为负数)=$\frac{1}{4}$;
(2)列表如下:
| -2 | 0 | 1 | 2 | |
| -2 | --- | -2 | -1 | 0 |
| 0 | -2 | --- | 1 | 2 |
| 1 | -1 | 1 | --- | 3 |
| 2 | 0 | 2 | 3 | --- |
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求解.注意从中任取一球,不放回是解题的关键.

练习册系列答案
相关题目
8.关于反比例函数y=-$\frac{4}{x}$,下列说法正确的是( )
| A. | 图象在第一、三象限 | B. | 图象经过点(2,-8) | ||
| C. | 当x>0时,y随x的增大而减小 | D. | 当x<0时,y随x的增大而增大 |
18.在反比例函数y=$\frac{1-3m}{x}$图象上有两点A(1,y1),B(2,y2),且y1>y2,则m的取值范围是( )
| A. | m$>\frac{1}{3}$ | B. | m$<\frac{1}{3}$ | C. | m$≥\frac{1}{3}$ | D. | m$≤\frac{1}{3}$ |
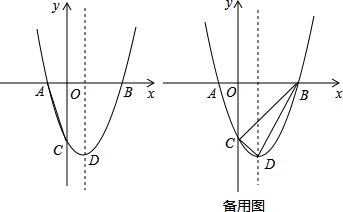
 如图,已知点B,D在反比例函数y=$\frac{a}{x}$(a>0)的图象上,点A,C在反比例函数y=$\frac{b}{x}$(b<0)的图象上,AB∥CD∥x轴,AB,CD在x轴的同侧,AB=4,CD=3,AB与CD的距离为1,则a-b的值是12.
如图,已知点B,D在反比例函数y=$\frac{a}{x}$(a>0)的图象上,点A,C在反比例函数y=$\frac{b}{x}$(b<0)的图象上,AB∥CD∥x轴,AB,CD在x轴的同侧,AB=4,CD=3,AB与CD的距离为1,则a-b的值是12.