题目内容
 如图,在矩形ABCD中,AB=2,AD=1,点P是边AB 上的一个动点,把△APD沿PD向矩形内折叠成△EPD,过E点作EF⊥BC于F,作EG⊥CD于G,如果四边形EFCG与矩形ABCD相似,则AP=
如图,在矩形ABCD中,AB=2,AD=1,点P是边AB 上的一个动点,把△APD沿PD向矩形内折叠成△EPD,过E点作EF⊥BC于F,作EG⊥CD于G,如果四边形EFCG与矩形ABCD相似,则AP=考点:相似多边形的性质,翻折变换(折叠问题)
专题:计算题
分析:延长GE交AB于H,如图,根据相似多边形的性质可得EF=2GE,则DG=CD-CG=2-GE,再利用折叠的性质得DE=AD+1,PA=PE,接着根据勾股定理得GE2+(2-GE)2=12,解得GE=
,于是可计算出DG=
,EH=GH-GE=
,设AP=x,则PE=x,PH=AH-AP=
-x,然后在Rt△PEH中,根据勾股定理得到(
)2+(
-x)2=x2,再解方程求出x的值即可.
| 3 |
| 5 |
| 4 |
| 5 |
| 2 |
| 5 |
| 4 |
| 5 |
| 2 |
| 5 |
| 4 |
| 5 |
解答:解:延长GE交AB于H,如图,
∵四边形EFCG与矩形ABCD相似,
∴
=
,即
=
,
∴EF=2GE,
∴CG=2GE,
∴DG=CD-CG=2-GE,
∵△APD沿PD向矩形内折叠成△EPD,
∴DE=AD+1,PA=PE,
在Rt△DGE中,∵GE2+DG2=DE2,
∴GE2+(2-GE)2=12,解得GE=
,
∴DG=
,EH=GH-GE=
,
设AP=x,则PE=x,PH=AH-AP=
-x,
在Rt△PEH中,∵EH2+PH2=PE2,
∴(
)2+(
-x)2=x2,解得x=
,
即AP的长为
.
故答案为
.
∵四边形EFCG与矩形ABCD相似,
∴
| GE |
| AD |
| EF |
| AB |
| GE |
| 1 |
| EF |
| 2 |

∴EF=2GE,
∴CG=2GE,
∴DG=CD-CG=2-GE,
∵△APD沿PD向矩形内折叠成△EPD,
∴DE=AD+1,PA=PE,
在Rt△DGE中,∵GE2+DG2=DE2,
∴GE2+(2-GE)2=12,解得GE=
| 3 |
| 5 |
∴DG=
| 4 |
| 5 |
| 2 |
| 5 |
设AP=x,则PE=x,PH=AH-AP=
| 4 |
| 5 |
在Rt△PEH中,∵EH2+PH2=PE2,
∴(
| 2 |
| 5 |
| 4 |
| 5 |
| 1 |
| 2 |
即AP的长为
| 1 |
| 2 |
故答案为
| 1 |
| 2 |
点评:本题考查了相似多边形的性质为:对应角相等;对应边的比相等.也考查了折叠的性质和勾股定理.

练习册系列答案
相关题目
 如图,在如图网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正切值是( )
如图,在如图网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正切值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列式子
a+b,S=
ab,5,m,8+y,m+3=2,
≥
中,代数式有( )
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 5 |
| 7 |
| A、6个 | B、5个 | C、4个 | D、3个 |
 数学老师布置10道选择题作为课堂练习,学习委员将全班同学的答欢迎登陆全品中考网“题情况绘制成条形图,据统计图可知,答对8道题的同学的频率是( )
数学老师布置10道选择题作为课堂练习,学习委员将全班同学的答欢迎登陆全品中考网“题情况绘制成条形图,据统计图可知,答对8道题的同学的频率是( )| A、0.38 | B、0.4 |
| C、0.16 | D、0.08 |
如果不等式组
的解是x>a,那么a的取值范围是( )
|
| A、a≥4 | B、a≤4 | C、a=4 |
如果a>b,那么下列不等式中不正确的是( )
| A、a-2>b-2 | ||||
B、
| ||||
| C、-2a<-2b | ||||
| D、a+1<b-1 |
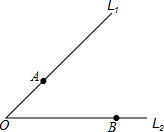 如图,由同一点O出发的两公交车分别沿道路L1、L2行驶且两公路分别经过A、B两个小区门口.
如图,由同一点O出发的两公交车分别沿道路L1、L2行驶且两公路分别经过A、B两个小区门口.