题目内容
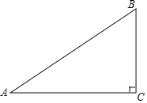
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,将
上,将![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 落在点
落在点![]() 处,当
处,当![]() 时,
时,![]() ________.
________.
【答案】![]() 或
或![]()
【解析】
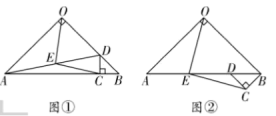
分两种情况进行讨论:①当A'在AC上方时,由折叠可得∠AED=∠A'ED,当A'E⊥AC时,∠AED=∠A'ED=45°,再过D作DF⊥AC于F,过B作BG⊥A'E于G,则△DEF是等腰直角三角形,再根据DF∥BC,D是AB的中点,BC=6,求得![]() ,最后根据等腰Rt△A'BG可得
,最后根据等腰Rt△A'BG可得![]() ;②当A'在AC下方时,也是作辅助线构造等腰直角三角形和矩形,利用勾股定理进行计算求解.
;②当A'在AC下方时,也是作辅助线构造等腰直角三角形和矩形,利用勾股定理进行计算求解.
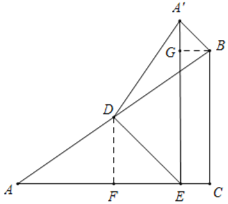
解:①如图所示,A'在AC上方,
∵在△ABC中,∠C=90°,AC=8,BC=6,
∴AB=10, 由折叠可得∠AED=∠A'ED,
当A'E⊥AC时,∠AED=∠A'ED=45°,
如图,过D作DF⊥AC于F,过B作BG⊥A'E于G,则△DEF是等腰直角三角形,
∵DF∥BC,D是AB的中点,AC=8,BC=6,
∴AF=CF=![]() AC=4,DF=
AC=4,DF=![]() BC=3,
BC=3,
∴EF=3,CE=![]() ,
,
∴矩形BCEG中,BG=CE=1,BC=EG=6,
∵AE=![]() , ∴A'E=7, ∴A'G=
, ∴A'E=7, ∴A'G=![]() ,即A'G=BG,
,即A'G=BG,
∴在等腰Rt△A'BG中,A'B=![]() .
.
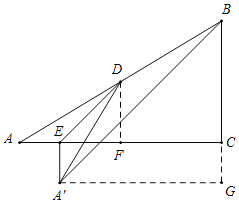
②如图所示,A'在AC的下方,过D作DF⊥AC于F,过A'作A'G⊥BC于G,
由折叠可得∠AED=∠A'ED,
当A'E⊥AC时,∠AED=∠A'ED=135°,∠A'EF=90°,故∠DEF=45°,即△DEF是等腰直角三角形,
∴DF=EF=![]() BC=3,
BC=3,
又∵AF=![]() AC=4,
AC=4,
∴AE=1,EC=![]() A'G,
A'G,
∵A'E=AE=1,
∴CG=1,BG=BC+CG=7,即A'G=BG,
∴在等腰Rt△A'BG中,A'B=![]() ,
,
故答案为:![]() 或
或![]() .
.

练习册系列答案
相关题目