题目内容
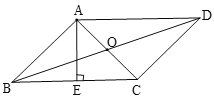
【题目】如图，在
中，
，
，
．点
从
出发沿
方向以每秒
的速度向终点
运动．点
从
出发沿
方向以每秒
的速度向点运动、同时当点运动停止时，点随之停止运动．过点作
交边
于点
，将
绕
的中点旋转180°得到
．过点作
交射线
于点
，以
为边向右下方作正方形
，设点的运动时间为
（秒）．
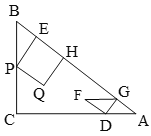
（1）直接写出
的长度（用含的代数式表示）．
（2）当点
落在
上时，求的值．
（3）当正方形与有重合部分时，求正方形与重合图形部分的周长
与时间的函数解析式．
（4）当直线
与的某一边垂直时，直接写出的值．
【答案】（1）
；（2）
；（3）当
时，
=52t-30；当
时，=12t；当
时，=-6t+15；（4）
，，
．
【解析】
（1）利用勾股定理可求出AB的长，可得cosA=
，利用距离=速度×时间可求出AD=5t，利用∠A的余弦值即可得答案；
（2）如图，由旋转的性质可得四边形AGFD是平行四边形，∠FDG=∠AGD=90°，可得∠HGF=∠A，根据三角函数的定义可得tan∠B=
，根据距离=速度×时间可求出BE=4t，利用∠B的正切值可用t表示出PE的长，由正方形的性质可得EH=PE，当点F落在
上时可得四边形FDGH是矩形，可得FD=HG，即可证明HG=AG，根据BE+EH+HG+AG=AB=10列方程即可求出t值；
（3）先分别求出DG与HQ重合、点F落在PE上、DG与PE重合时的t值，再根据各时间段中l与t当关系式即可；
（4）分QF⊥BC、QF⊥AB、QF⊥AC三种情况，利用∠A的三角函数及线段的和差关系分别求出t值即可．
（1）∵AC=8，BC=6，
∴AB=
=10，
∴cos∠A=，sin∠A=
，tan∠A=
，
∵点D的速度为每秒5cm，
∴AD=5t，
∴AG=AD·cosA=5t×=4t．
（2）∵将
绕
的中点旋转180°得到
，
∴四边形AGFD是平行四边形，∠FDG=∠AGD=90°，AG=FD，
∵点
落在上，DG⊥AB，四边形EPQH是正方形，
∴∠FHG=∠DGH=∠FDG=90°，
∴四边形FDGH是矩形，
∴FD=HG，
∴HG=AG=4t，
∵AC=8，BC=6，∠BCA=90°，
∴tan∠B=
=，
∵点E的速度为每秒4cm，
∴BE=4t，
∴PE=BE·tan∠B=
t，
∵四边形EPQH是正方形，
∴EH=PE=t，
∵BE+EH+HG+AG=AB=10，
∴4t+t+4t+4t=10，
解得：．
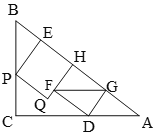
（3）∵AD=5t，AG=4t，
∴DG=3t，
如图，当DG与HQ重合时，
∵BE=4t，EH=PE=t，AG=4t，
∴4t+t+4t=10，
解得：t=，
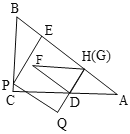
如图，当点F落在PE上时，
∵BE=4t，EG=DF=4t，AG=4t，
∴4t+4t+4t=10，
解得：t=
，
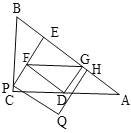
如图，当DG与PE重合时，
∵BE=4t，AG=4t，
∴4t+4t=10，
解得：t=
，
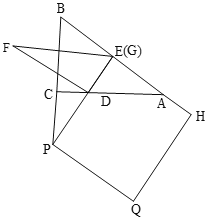
①如图，当时，FD、FG分别交QH于M、N，
∵BE=4t，EH=PE=t，AG=4t，
∴HG=10-4t-4t-t=10-
t，
∵四边形MDGH是矩形，
∴MB=GH=10-t，
∴FM=FD-MD=4t-(10-t)=
t-10，
∵∠F=∠A，
∴MN=FM·tan∠A=FM=13t-
，FN=
=FM=
，
∴l=FM+MN+FN=52t-30．
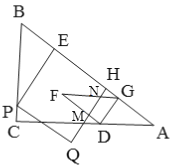
②当时，重合部分的周长即是△FDG当周长，
∴l=3t+4t+5t=12t．
③如图，当时，FD、FG分别交PE于M、N，
∵BE=4t，AG=4t，
∴EG=MD=10-8t，
∵∠EGN=∠A，
∴NE=EG·tan∠A=-6t，NG=
=
-10t，
∴MN=MN-NE=DG-NE=3t-（-6t）=9t-，
∴l=MN+NG+DG+MD=9t-+-10t+3t+10-8t=-6t+15，
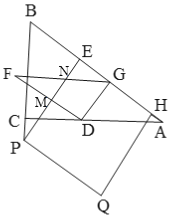
综上所述：当时，l=52t-30；当时，l=12t；当时，l= -6t+15．
（4）①如图，当FQ⊥BC时，
∵四边形AGFD是平行四边形，
∴FG//AC，
∵∠BCA=90°，
∴GF⊥BC，
∴点Q在直线GF上，
∵AG=4t， QH=PE=EH=t，
∴HG=10-4t-4t-t=10-t，
∵∠FDN=∠A，
∴QH=HG·tan∠A，即t=（10-t），
解得：，
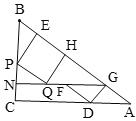
②由（2）可知，当点F落在QH上时，DF⊥AB，此时，
③如图，当FQ⊥AC时，直线FQ交AB于M，
∵FQ⊥AC，FG//AC，
∴FQ⊥FG，
∵∠A+∠QMH=90°，∠MQH+∠QMH=90°，
∴∠MQH=∠A，
∵QH=PE=t，FG=AD=5t，
∴MH=QH·tan∠A=4t，MG=
=
t，
∵BE=4t，AG=4t，EH=t，
∴HG=10-t，
∵MG=MH+HG，即t=4t+10-t，
解得：，
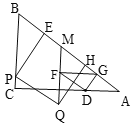
综上所述：直线
与
的某一边垂直时，或或．
