Question

【题目】如图，已知点A的坐标为（4，0），点B的坐标为（0，3），在第一象限内找一点P(a,b) ,使△PAB为等边三角形，则2(a-b)=___________．

Answer 1

【答案】

【解析】

根据A、B坐标求出直线AB的解析式后，求得AB中点M的坐标，连接PM，在等边△PAB中，M为AB中点，所以PM⊥AB，，再求出直线PM的解析式，求出点P坐标；在Rt△PAM中，AP=AB=5，，即且a＞0，解得a>0，即，将a代入直线PM的解析式中求出b的值，最后计算2(a-b)的值即可；

解：∵A(4，0)，B(0，3)，

∴AB=5，

设，

∴，

∴ ，

∴，

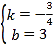∵A(4，0) B(0，3) ，

∴AB中点，连接PM，

在等边△PAB中，M为AB中点，

∴PM⊥AB，，

∴，

∴设直线PM的解析式为，

∴，

∴，

∴，

∴，

在Rt△PAM中，AP=AB=5，

∴，

∴，

∴，

∴，

∵a>0，

∴，

∴，

∴；