题目内容
【题目】有一组邻边相等的凸四边形叫做“和睦四边形”,寓意是全世界和平共处,睦邻友好,共同发展.如菱形,正方形等都是“和睦四边形”.
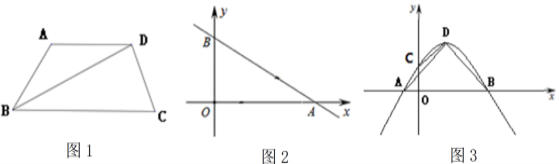
(1)如图1,BD平分∠ABC,AD∥BC,求证:四边形ABCD为“和睦四边形”;
(2)如图2,直线![]() 与x轴、y轴分别交于A、B两点,点P、Q分别是线段OA、AB上的动点.点P从点A出发,以每秒4个单位长度的速度向点O运动.点Q从点A出发,以每秒5个单位长度的速度向点B运动.P、Q两点同时出发,设运动时间为t秒.当四边形BOPQ为“和睦四边形”时,求t的值;
与x轴、y轴分别交于A、B两点,点P、Q分别是线段OA、AB上的动点.点P从点A出发,以每秒4个单位长度的速度向点O运动.点Q从点A出发,以每秒5个单位长度的速度向点B运动.P、Q两点同时出发,设运动时间为t秒.当四边形BOPQ为“和睦四边形”时,求t的值;
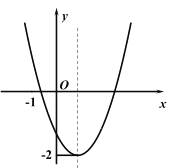
(3)如图3,抛物线![]() 与
与![]() 轴交于A、B两点(点A在点B的左侧),与y轴交于点
轴交于A、B两点(点A在点B的左侧),与y轴交于点![]() ,抛物线的顶点为点D.当四边形COBD为“和睦四边形”,且CD=OC.抛物线还满足:①
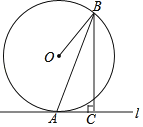
,抛物线的顶点为点D.当四边形COBD为“和睦四边形”,且CD=OC.抛物线还满足:①![]() ;②顶点D在以AB为直径的圆上. 点
;②顶点D在以AB为直径的圆上. 点![]() 是抛物线
是抛物线![]() 上任意一点,且
上任意一点,且![]() .若
.若![]() 恒成立,求m的最小值.
恒成立,求m的最小值.
【答案】(1)见解析;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)由BD平分∠ABC推出∠ABD=∠CBD,又AB∥BC,所以∠ADB=∠CBD,所以∠ABD=∠ADB,即AB=AD,所以四边形ABCD为“和睦四边形”; (2)分别求出 AQ、AP、BQ、OP、OB的值,连接PQ ,因为![]()
![]() ,所以
,所以![]() ,所以
,所以![]()
![]() ,根据勾股定理求出PQ,再分类讨论t的值即可;(3)表示出点
,根据勾股定理求出PQ,再分类讨论t的值即可;(3)表示出点![]() 的坐标,由
的坐标,由![]() 可得,
可得,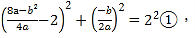 因为
因为![]() 得出
得出![]() 所以
所以![]() ,即
,即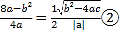 ,由①②的方程,且
,由①②的方程,且![]() 解出a、b的值,求出抛物线的解析式为
解出a、b的值,求出抛物线的解析式为![]() ,因为P在抛物线上,将P代入抛物线得,
,因为P在抛物线上,将P代入抛物线得,![]() ,可得
,可得![]() 当
当![]() ,又因为
,又因为![]() ,所以
,所以![]() ,即
,即![]() ,得出m的最小值为
,得出m的最小值为![]() ;
;
解:
(1)![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形ABCD为“和睦四边形”;
四边形ABCD为“和睦四边形”;
(2)由题意得:AQ=5 t ,AP=4 t ,BQ=10 - 5 t ,OP=8 - 4 t ,OB=6,连接PQ ,
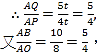
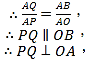
![]() ,
,
![]() ,
,
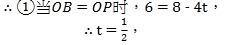


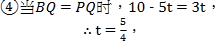
综上:![]() ;
;
(3)由题意得:![]() ,
,
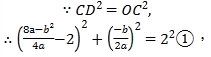
![]()
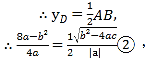
由①②,且![]() ,得
,得![]() ,
,
![]() ,
,
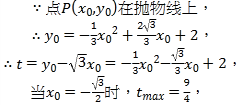
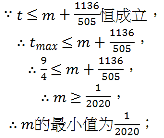

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目