题目内容
17．在数学活动课上，同学们要判断一个四边形门框是否为矩形，下面是某学习小组拟定的方案，其中正确的是（ ）| A． | 测量对角线是否相互垂直 | B． | 测量两组对边是否分别相等 | ||
| C． | 测量对角线是否相等 | D． | 测量其中三个角是否都为直角 |
分析 矩形的判定定理有：
（1）有一个角是直角的平行四边形是矩形；
（2）有三个角是直角的四边形是矩形；
（3）对角线互相平分且相等的四边形是矩形．
解答 解：A、对角线是否垂直，不能判定四边形是矩形，故此选项错误；
B、两组对边是否分别相等，能判定平行四边形，故此选项错误；
C、对角线是否相等，不能判定四边形是矩形，故此选项错误；
D、其中四边形中三个角都为直角，能判定矩形，故此选项正确．
故选：D．
点评 本题考查的是矩形的判定定理，解题的关键是牢记这些定理，属于基础概念题，比较简单．
练习册系列答案
相关题目
如图，在等腰△ABC中，AB=AC，点D、E分别在边AB、AC上，BE与CD交于点O，且BO=CO，求证：
如图，菱形ABCD中，E为BC延长线上一点，连接AE，∠E=∠B，过点D作DH⊥AE于H．
5．如图1，在矩形ABCD中，AB=12cm，BC=10cm，点P从A出发，沿A→B→C→D的路线运动，到D停止；点Q从D点出发，沿D→C→B→A路线运动，到A点停止．若点P，点Q同时出发，点P的速度为1cm/s，点Q的速度为2cm/s，a秒后点P改变速度，变为bcm/s，点Q速度不变．图2是点P出发x秒后△APD的面积S（cm2）与x（s）的函数关系图象，根据图象判断，下列选项正确的是（ ）
| A． | a=5s | B． | 点P改变速度后4s与点Q相遇 | ||
| C． | b=3cm/s | D． | c=18s |
2．用反证法证明“a∥b，b∥c，则a∥c”时，第一步应先假设（ ）
| A． | a不平行于c | B． | b不平行于c | C． | a⊥c | D． | b⊥c |
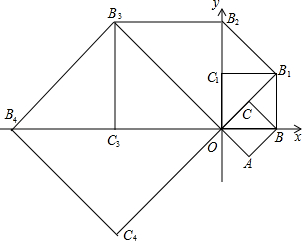如图，在平面直角坐标系xOy中，有一边为1的正方形OABC，点B在x轴的正半轴上，如果以对角线OB为边作第二个正方形OBB1C1，再以对角线OB1为边作第三个正方形OB1B2C2，…，照此规律作下去，则B2的坐标是（0，2$\sqrt{2}$）；B2015的坐标是（${2}^{254}\sqrt{2}$，-${2}^{254}\sqrt{2}$）．