��Ŀ����
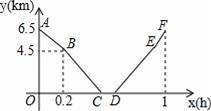
�Ӽص��ҵأ�����һ������·��Ȼ����һ��ƽ·��С���ﳵ�Ӽس����������ҵغ���Ϣһ��ʱ�䣬Ȼ��ԭ·���ؼأ�����С���ﳵ�����¡�ƽ·������ʱ�ֱ𱣳�����ǰ������֪С���ﳵ���µ��ٶȱ�ƽ·�ϵ��ٶ�ÿСʱ��5km�����µ��ٶȱ���ƽ·�ϵ��ٶ�ÿСʱ��5km����С������xh�������ҵ�ykm�ĵط���ͼ�е�����ABCDEF��ʾy��x֮��ĺ�����ϵ��
��1��С���ﳵ��ƽ·�ϵ��ٶ�Ϊ�� ��km/h�������ҵ���Ϣ���� ��h��
��2���ֱ����߶�AB��EF����Ӧ�ĺ�����ϵʽ��
��3���Ӽص��ҵؾ������أ����С�����ξ������ص�ʱ����Ϊ0.85h����������֮���·�̣�

�����㡿һ�κ�����Ӧ�ã�
����������1���ֱ�����С���ﳵ���µ��ٶȣ�С��ƽ·�ϵ��ٶȣ�С�����µ��ٶȣ�С��ƽ·�����õ�ʱ�䣬С���������õ�ʱ��Ϊ�����ɽ��
��2���������µ��ٶ�Ϊ10km/h�����µ��ٶ�Ϊ20km/h�������߶�AB����Ӧ�ĺ�����ϵʽΪ��y=6.5��10x���߶�EF����Ӧ�ĺ�����ϵʽΪy=4.5+20��x��0.9�������ɽ��
��3����С������aСʱ��һ�ξ������أ���������õ�6.5��10a=20��a+0.85����13.5�����a��ֵ�����ɽ��
����𡿽⣺��1��С���ﳵ���µ��ٶ�Ϊ����6.5��4.5����0.2=10��km/h����
С��ƽ·�ϵ��ٶ�Ϊ��10+5=15��km/h����
С�����µ��ٶ�Ϊ��15+5=20��km/h����
С��ƽ·�����õ�ʱ��Ϊ��2��4.5��15��=0.6h��
С���������õ�ʱ��Ϊ����6.5��4.5����20=0.1h
����С�����ҵ���Ϣ�ˣ�1��0.1��0.6��0.2=0.1��h����
�ʴ�Ϊ��15��0.1��
��2���������֪�����µ��ٶ�Ϊ10km/h�����µ��ٶ�Ϊ20km/h��
�����߶�AB����Ӧ�ĺ�����ϵʽΪ��y=6.5��10x��
��y=��10x+6.5��0��x��0.2����
�߶�EF����Ӧ�ĺ�����ϵʽΪy=4.5+20��x��0.9����
��y=20x��13.5��0.9��x��1����
��3���������֪��С����һ�ξ���������AB�Σ��ڶ��ξ���������EF�Σ�
��С������aСʱ��һ�ξ������أ�
��С��������a+0.85��Сʱ�ڶ��ξ������أ�
6.5��10a=20��a+0.85����13.5
��ã�a=
 ��
��

 =1��ǧ�ף���
=1��ǧ�ף���
�𣺱������֮���·��Ϊ1ǧ�ף�
�����������⿼����һ�κ�����Ӧ�ã��������Ĺؼ��Ƕ�������ͼ�����һ�κ����Ľ���ʽ��
��

 ���
�в��� ��һ�����
��һ����� ��ֵΪ ( )
��ֵΪ ( )





 ��
�� �Ĵ���ͼ���� �� ��
�Ĵ���ͼ���� �� ��
 �Ǻ���
�Ǻ��� ��
�� ��
�� ���ķ���������
���ķ��������� ����
���� �� ��
�� �� B.
B. C.
C. D.
D.