题目内容
 在长方形ABCD中,M是CD边的中点,弧DN是以A为圆心的一段圆弧,弧KN是以B为圆心的一段圆弧,AN=a,BN=b,则图中阴影部分的面积是
在长方形ABCD中,M是CD边的中点,弧DN是以A为圆心的一段圆弧,弧KN是以B为圆心的一段圆弧,AN=a,BN=b,则图中阴影部分的面积是分析:设阴影部分面积为S,则S可以通过长方形的面积减去两个圆弧的面积及一个三角形的面积间接求得.
解答:解:根据题意S矩形ABCD=a(a+b),设阴影面积为S,
则阴影部分的面积是:S=a(a+b)-
(a2+b2)-
(a-b),
=a2+ab-
a2-
b2-
+
,
=ab-
a2-
b2.
故答案为:ab-
a2-
b2.
则阴影部分的面积是:S=a(a+b)-
| π |
| 4 |
| (a+b) |
| 4 |
=a2+ab-
| π |
| 4 |
| π |
| 4 |
| a2 |
| 4 |
| b2 |
| 4 |
=ab-
| (π-3) |
| 4 |
| (π-1) |
| 4 |
故答案为:ab-
| (π-3) |
| 4 |
| (π-1) |
| 4 |
点评:本题考查了整式的加减,属于基础题,难度不大,注意面积的间接求法.

练习册系列答案
相关题目
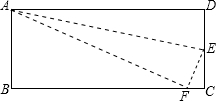
 已知:如图,在长方形ABCD中,AB=3,BC=4将△BCD沿BD所在直线翻折,使点C落在点F上,如果BF交AD于E,求AE的长.
已知:如图,在长方形ABCD中,AB=3,BC=4将△BCD沿BD所在直线翻折,使点C落在点F上,如果BF交AD于E,求AE的长. 在长方形ABCD中,∠BDC=32°,将△ABD沿BD所在直线折叠,使点A落在E处,则∠CDE=
在长方形ABCD中,∠BDC=32°,将△ABD沿BD所在直线折叠,使点A落在E处,则∠CDE= 如图,在长方形ABCD中,点E在BC上,点F在CD上,已知AB=6,AD=5,BE=2,CF=1,连接AE、EF、AF
如图,在长方形ABCD中,点E在BC上,点F在CD上,已知AB=6,AD=5,BE=2,CF=1,连接AE、EF、AF 如图,在长方形ABCD中,点Q在边CD上(不与点C、D重合),将长方形ABCD绕点Q顺时针旋转90°后,得到长方形A1B1C1D1,且重叠部分的四边形PCQD1是长方形.如果AB=a,BC=b,CQ=x.(b>a>0)
如图,在长方形ABCD中,点Q在边CD上(不与点C、D重合),将长方形ABCD绕点Q顺时针旋转90°后,得到长方形A1B1C1D1,且重叠部分的四边形PCQD1是长方形.如果AB=a,BC=b,CQ=x.(b>a>0)