题目内容
 如图,在长方形ABCD中,点Q在边CD上(不与点C、D重合),将长方形ABCD绕点Q顺时针旋转90°后,得到长方形A1B1C1D1,且重叠部分的四边形PCQD1是长方形.如果AB=a,BC=b,CQ=x.(b>a>0)
如图,在长方形ABCD中,点Q在边CD上(不与点C、D重合),将长方形ABCD绕点Q顺时针旋转90°后,得到长方形A1B1C1D1,且重叠部分的四边形PCQD1是长方形.如果AB=a,BC=b,CQ=x.(b>a>0)(1)用含有a、b、x的代数式表示△QDC1的面积S1和△A1BP的面积S2.
(2)求六边形ABA1B1C1D的面积S,并进行化简.
分析:(1)由ABCD为矩形,得到AB=DC=a,BC=AD=b,由CD-CQ=QD表示出QD,利用三角形的面积公式表示△QDC1的面积S1即可;由BC-CP=BP,表示出BP,由A1D1-PD1=A1P,表示出AP1,利用三角形的面积公式表示出△A1BP的面积S2即可;
(2)六边形的面积=△QDC1的面积+△A1BP的面积+两个矩形ABCD的面积-矩形PCQD1的面积,列出关系式,去括号合并即可得到结果.
(2)六边形的面积=△QDC1的面积+△A1BP的面积+两个矩形ABCD的面积-矩形PCQD1的面积,列出关系式,去括号合并即可得到结果.
解答:解:(1)根据题意列得:S1=
x(a-x);S2=
(b-x)(b-a+x);
(2)S=
x(a-x)+
(b-x)(b-a+x)+2ab-x(a-x)
=
ax-
x2+
(b2-ab+bx-bx+ax-x2)+2ab-ax+x2
=
ax-
x2+
b2-
ab+
bx-
bx+
ax-
x2+2ab-ax+x2
=
b2+
ab.
| 1 |
| 2 |
| 1 |
| 2 |
(2)S=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3 |
| 2 |
点评:此题考查了整式加减运算的应用,弄清题意是解本题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
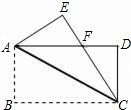 于点F.
于点F. 如图,在Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,以D作DE⊥AC与CB的延长线交于E,以AB、BE为邻边作长方形ABEF,连接DF,求DF的长.
如图,在Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,以D作DE⊥AC与CB的延长线交于E,以AB、BE为邻边作长方形ABEF,连接DF,求DF的长.

