题目内容
 已知:如图,在长方形ABCD中,AB=3,BC=4将△BCD沿BD所在直线翻折,使点C落在点F上,如果BF交AD于E,求AE的长.
已知:如图,在长方形ABCD中,AB=3,BC=4将△BCD沿BD所在直线翻折,使点C落在点F上,如果BF交AD于E,求AE的长.
分析:设AE=x,分别可求得DE,BE与DE的长,易得△AEB∽△DEF;可以列出比例关系式,代入数据解可得答案.
解答:解:设AE=x,DE=4-x,
根据勾股定理可得:
BE=
,
故EF=BF-BE=BC-BE=4-
.
∵△AEB∽△DEF,
∴
=
.
∵AB=3,BC=4,
∴x=
.
即AE=
.
根据勾股定理可得:
BE=
| x2+9 |
故EF=BF-BE=BC-BE=4-
| x2+9 |
∵△AEB∽△DEF,
∴
| AE |
| EF |
| BE |
| DE |
∵AB=3,BC=4,
∴x=
| 7 |
| 8 |
即AE=
| 7 |
| 8 |
点评:解答本题要充分利用正方形的特殊性质.注意在正方形中的特殊三角形的应用,搞清楚矩形、菱形、正方形中的三角形的三边关系,可有助于提高解题速度和准确率.

练习册系列答案
相关题目
 已知:如图,将长方形纸片沿着CE所在直线对折,B点落在点B′处,CD与E B′交于点F,如果AB=10cm,AD=6cm,AE=2cm,求EF的长.
已知:如图,将长方形纸片沿着CE所在直线对折,B点落在点B′处,CD与E B′交于点F,如果AB=10cm,AD=6cm,AE=2cm,求EF的长.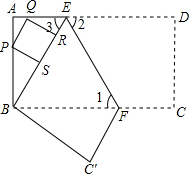 已知:如图,把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C′的位置上.若∠1=60°,AE=1.
已知:如图,把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C′的位置上.若∠1=60°,AE=1. 已知:如图,在长方形ABCD中,AB=3,BC=4将△BCD沿BD所在直线翻折,使点C落在点F上,如果BF交AD于E,求AE的长.
已知:如图,在长方形ABCD中,AB=3,BC=4将△BCD沿BD所在直线翻折,使点C落在点F上,如果BF交AD于E,求AE的长.