题目内容
半径为2cm 的⊙O中有长为2 cm的弦AB,则弦AB所对的圆周角度数为( )
cm的弦AB,则弦AB所对的圆周角度数为( )
| A.600 | B.900 | C.600或1200 | D.450或900 |
C
解析试题分析:首先根据题意画出图形,作OD⊥AB,通过垂径定理,即可推出∠AOD的度数,求得∠AOB的度数,然后根据圆周角定理,即可推出∠AMB和∠ANB的度数。
解:连接OA,做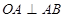 :
:
OA=2,AB=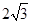
AB=AD= ,
,
∴∠AOD=60°,
∴∠AOB=120°,
∴∠AMB=60°,
∴∠ANB=120°.
∴弦AB所对的圆周角度数为60°或120°.
故选C.
考点:圆周角定理;垂径定理
点评:本题主要考查圆周角定理、垂径定理,关键在于根据题意正确的画出图形,运用圆周角定理和垂径定理认真的进行分析.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 如图,在半径为2cm的⊙O中有长为2
如图,在半径为2cm的⊙O中有长为2| 3 |
| A、60° | B、90° |
| C、120° | D、150° |
 如图是一个高为2
如图是一个高为2| 15 |
(计算结果保留3个有效数字.参考数据
| 2 |
| 3 |
| A、3.12cm |
| B、3.28cm |
| C、3.31cm |
| D、3.00cm |
 如图,求中心点为原点,顶点A、D在x轴上,半径为2cm的正六边形ABCDEF的各个顶点的坐标.
如图,求中心点为原点,顶点A、D在x轴上,半径为2cm的正六边形ABCDEF的各个顶点的坐标. 如图是一个高为
如图是一个高为