题目内容
2.二次函数y=a(x-4)2,当自变量x由0增加到2时,函数值增加6(1)求出此函数关系式;
(2)说明函数值y随x值的变化情况.
分析 (1)利用x=0和x=2的函数值的差为6列方程得到a(2-4)2-a(0-4)2=6,解得a=-$\frac{1}{2}$,从而可确定函数解析式;
(2)根据二次函数的性质求解.
解答 解:(1)根据题意得a(2-4)2-a(0-4)2=6,解得a=-$\frac{1}{2}$,
所以函数解析式为y=-$\frac{1}{2}$(x-4)2;
(2)抛物线的对称轴为直线x=4,
所以当x<4时,y随x的增大而增大;当x>4时,y随x的增大而减小.
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
该商场计划购进两种手机若干部,共需15.5万元,预计全部销售后获毛利润共2.1万元(毛利润=(售价-进价)×销售量)
(1)该商场计划购进甲、乙两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量,已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,设甲种手机减少x部,求y的解析式.
(3)该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
| 甲 | 乙 | |
| 进价(元/部) | 4000 | 2500 |
| 售价(元/部) | 4300 | 3000 |
(1)该商场计划购进甲、乙两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量,已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,设甲种手机减少x部,求y的解析式.
(3)该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
7. 如图是由几个相同的小正方体搭成的几何体的主视图和俯视图,则搭成这个几何体的小正方体的个数最少是( )
如图是由几个相同的小正方体搭成的几何体的主视图和俯视图,则搭成这个几何体的小正方体的个数最少是( )
 如图是由几个相同的小正方体搭成的几何体的主视图和俯视图,则搭成这个几何体的小正方体的个数最少是( )
如图是由几个相同的小正方体搭成的几何体的主视图和俯视图,则搭成这个几何体的小正方体的个数最少是( )| A. | 12个 | B. | 10个 | C. | 8个 | D. | 6个 |
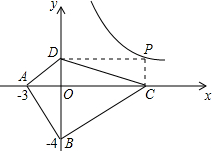 如图,已知A(-3,0),B(0,-4),P为双曲线y=$\frac{12}{x}$(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.则四边形ABCD面积的最小值为24.
如图,已知A(-3,0),B(0,-4),P为双曲线y=$\frac{12}{x}$(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.则四边形ABCD面积的最小值为24.