题目内容
 如图,长方形ABCD中,AB=10,BC=5,在CD上是否存在点P,使∠APB=90°?试说明理由.
如图,长方形ABCD中,AB=10,BC=5,在CD上是否存在点P,使∠APB=90°?试说明理由.考点:相似三角形的判定与性质,根的判别式,圆周角定理
专题:
分析:如图,证明∠DAP=∠BPC,结合∠D=∠C,得到△ADP∽△PCB;列出比例式
=
,求出DP即可解决问题.
| DP |
| BC |
| AD |
| PC |
解答: 解:存在点P,使∠APB=90°;理由如下:
解:存在点P,使∠APB=90°;理由如下:
如图,∵四边形ABCD为矩形,
∴∠D=∠C=90°,AD=BC=5,DC=AB=10;
设DP=λ,则PC=10-λ;
∵∠APB=90°,
∴∠APD+∠DAP=∠APD+∠BPC,
∴∠DAP=∠BPC,而∠D=∠C,
∴△ADP∽△PCB,
∴
=
,即
=
,
解得:λ=5,
即当DP=5时,∠APB=90°.
 解:存在点P,使∠APB=90°;理由如下:
解:存在点P,使∠APB=90°;理由如下:如图,∵四边形ABCD为矩形,
∴∠D=∠C=90°,AD=BC=5,DC=AB=10;
设DP=λ,则PC=10-λ;
∵∠APB=90°,
∴∠APD+∠DAP=∠APD+∠BPC,
∴∠DAP=∠BPC,而∠D=∠C,
∴△ADP∽△PCB,
∴
| DP |
| BC |
| AD |
| PC |
| λ |
| 5 |
| 5 |
| 10-λ |
解得:λ=5,
即当DP=5时,∠APB=90°.
点评:该题是一道条件探究型命题;以考查相似三角形的判定及其性质等几何知识点为核心构造而成;解题的关键是牢固掌握相似三角形的判定及其性质.

练习册系列答案
相关题目
将?ABCD绕O点旋转到?A′B′C′D′的位置,错误的是( )
| A、AB=A′B′ |
| B、AB一定平行于A′B′ |
| C、∠B=∠B′ |
| D、△ABC≌△A′B′C′ |
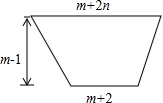 如图所示,一条水渠的横截面是一个下窄上宽的梯形,河底宽(m+2)米,渠宽(m+2n)米,求表示水渠横截面面积S的代数式,并求出当m=4,n=0.5时S的值.
如图所示,一条水渠的横截面是一个下窄上宽的梯形,河底宽(m+2)米,渠宽(m+2n)米,求表示水渠横截面面积S的代数式,并求出当m=4,n=0.5时S的值.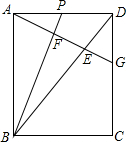 如图,在矩形ABCD中,P是AD上一动点,过点A作BP的垂线,垂足为F,交BD于点E,交CD于点G.
如图,在矩形ABCD中,P是AD上一动点,过点A作BP的垂线,垂足为F,交BD于点E,交CD于点G. 在△ABC中,AD是∠A的平分线,DE∥AB,在AB上截取BF=AE.试证明EF=BD.
在△ABC中,AD是∠A的平分线,DE∥AB,在AB上截取BF=AE.试证明EF=BD.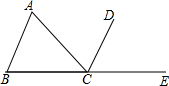 如图所示,在△ABC中,以C为顶点,在△ABC外作∠ACD=∠A,且点A和点D在直线BC的同侧,延长BC至E,在所作的图形中:
如图所示,在△ABC中,以C为顶点,在△ABC外作∠ACD=∠A,且点A和点D在直线BC的同侧,延长BC至E,在所作的图形中: