题目内容
6. 如图,矩形ABCD中,对角线AC和BD相交于点O,过O作EF⊥AC,交AD于E,交BC于F,连接AF、CE.
如图,矩形ABCD中,对角线AC和BD相交于点O,过O作EF⊥AC,交AD于E,交BC于F,连接AF、CE.(1)求证:四边形AECF是菱形
(2)若AB=3,BC=4,则菱形AECF的周长?
分析 (1)利用已知条件和矩形的性质易证△AEO≌△CFO,进而可得四边形AECF是平行四边形,又因为EF⊥AC,所以可证明四边形AECF是菱形
(2)设AE=CE=x,则DE=4-x,在直角三角形EDC中,利用勾股定理可求出x的值,进而可求出菱形的周长.
解答 (1)证明:∵四边形ABCD是矩形,
∴AO=CO,AD∥BC,
∴∠OAE=∠OCF,
∵EF⊥AC,
∴∠AOE=∠COF=90°,
在△AEO和△CFO中,
$\left\{\begin{array}{l}{∠OAE=∠OCF}\\{AO=CO}\\{∠AOE=∠COF}\end{array}\right.$,
∴△AEO≌△CFO,
∴OE=OF,
∵AO=CO,
∴四边形AECF是平行四边形,
∵EF⊥AC,
∴四边形AECF是菱形;
(2)解:∵四边形ABCD是矩形,
∴AB=CD=3,BC=AD=4,
AE=CE=x,则DE=4-x,在直角三角形EDC中由勾股定理可得:CE2=DE2+CD2,
即a2=(4-a)2+32,
解得:a=$\frac{25}{8}$,
∴菱形AECF的周长=4×$\frac{25}{8}$=12.5.
点评 本题考查了矩形的性质、菱形的判定和性质以及勾股定理的运用,熟记各种特殊四边形的判定方法和性质是解题关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
14.若将代数式中的任意两个字母交换,代数式不变,则称这个代数式为完全对称式,如a+b+c就是完全对称式.下列三个代数式:
①(a-b)2;
②(2a-b)(2a+b);
③a(a+b).
其中是完全对称式的是( )
①(a-b)2;
②(2a-b)(2a+b);
③a(a+b).
其中是完全对称式的是( )
| A. | ③ | B. | ①③ | C. | ②③ | D. | ① |
15.下列实数是无理数的是( )
| A. | $\frac{\sqrt{4}}{3}$ | B. | 0 | C. | 0.$\stackrel{•}{7}$ | D. | $\root{3}{9}$ |
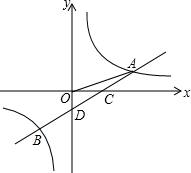 如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知OA=$\sqrt{10}$,tan∠AOC=$\frac{1}{3}$,点B的坐标为(m,-2).
如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知OA=$\sqrt{10}$,tan∠AOC=$\frac{1}{3}$,点B的坐标为(m,-2). 请按要求,只用无刻度的直尺作图(请保留画图痕迹,不写作法)如图,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是平行四边形,在图中画出∠AOB的平分线.
请按要求,只用无刻度的直尺作图(请保留画图痕迹,不写作法)如图,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是平行四边形,在图中画出∠AOB的平分线.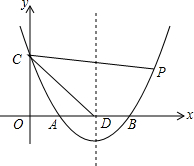 如图,抛物线y=$\frac{1}{3}$(x-$\sqrt{3}$)(x-3$\sqrt{3}$)与x轴交于A,B两点,与y轴交于点C,点D是抛物线的对称轴l与x轴的交点,点P是抛物线上一点,且∠DCP=30°,则符合题意的点P的坐标为($\frac{11\sqrt{3}}{3}$,$\frac{16}{9}$).
如图,抛物线y=$\frac{1}{3}$(x-$\sqrt{3}$)(x-3$\sqrt{3}$)与x轴交于A,B两点,与y轴交于点C,点D是抛物线的对称轴l与x轴的交点,点P是抛物线上一点,且∠DCP=30°,则符合题意的点P的坐标为($\frac{11\sqrt{3}}{3}$,$\frac{16}{9}$).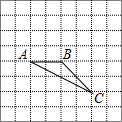 如图,在8×8的正方形网格中,△ABC的顶点在边长为1的小正方形的顶点上.
如图,在8×8的正方形网格中,△ABC的顶点在边长为1的小正方形的顶点上.