题目内容
16.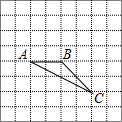 如图,在8×8的正方形网格中,△ABC的顶点在边长为1的小正方形的顶点上.
如图,在8×8的正方形网格中,△ABC的顶点在边长为1的小正方形的顶点上.(1)填空:∠ABC=135°,BC=2$\sqrt{2}$;
(2)若点A在网格所在的坐标平面里的坐标为(-2,0),请你在图中找出一点D,使以A、B、C、D四个点为顶点的平行四边形,满足条件的D点的坐标可以是(0,-2)(答案不唯一)(写出一个即可).
分析 (1)根据正方形的性质容易得出∠ABC的度数,由勾股定理求出BC即可;
(2)由点A的坐标得出坐标系,即可得出点D的坐标.
解答 解:(1)∠ABC=90°+45°=135°,BC=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$;
故答案为:135°,2$\sqrt{2}$;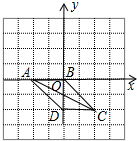
(2)∵A的坐标为(-2,0),
∴坐标系如图所示:
当CD∥AB,CD=AB=2时,四边形ABCD是平行四边形,
点D的坐标为(0,-2);
故答案为:(0,-2)(答案不唯一).
点评 本题考查了平行四边形的判定、坐标与图形性质、勾股定理;熟练掌握平行四边形的判定和勾股定理是解决问题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案
相关题目
11.下列运算中,正确的是( )
| A. | 3a-2a=a | B. | (a2)3=a5 | C. | a2•a3=a6 | D. | a10÷a5=a2 |
 如图,矩形ABCD中,对角线AC和BD相交于点O,过O作EF⊥AC,交AD于E,交BC于F,连接AF、CE.
如图,矩形ABCD中,对角线AC和BD相交于点O,过O作EF⊥AC,交AD于E,交BC于F,连接AF、CE. 如图,B处在A处的南偏西40°方向,C处在A处的南偏东12°方向,C处在B处得北偏东80°方向,则∠ACB的度数为88度.
如图,B处在A处的南偏西40°方向,C处在A处的南偏东12°方向,C处在B处得北偏东80°方向,则∠ACB的度数为88度. 如图,点E在AC的延长线上,图中能判断AB∥CD的条件是∠1=∠7或∠6=∠2或∠1+∠ACD=180°(只需写三个).
如图,点E在AC的延长线上,图中能判断AB∥CD的条件是∠1=∠7或∠6=∠2或∠1+∠ACD=180°(只需写三个).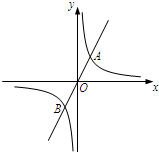 如图,正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$的图象交于点A、B,AB=2$\sqrt{5}$,
如图,正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$的图象交于点A、B,AB=2$\sqrt{5}$,