题目内容
 甲从A出发向B行走,同时乙从B出发向A行走,如图相交于点P的两条线段里l1、l2分别表示甲、乙距离B的路程y(km)与已用时间x(h)之间的关系.
甲从A出发向B行走,同时乙从B出发向A行走,如图相交于点P的两条线段里l1、l2分别表示甲、乙距离B的路程y(km)与已用时间x(h)之间的关系.(1)求甲乙行走的速度;
(2)求l1、l2的表达式;
(3)计算乙需多长时间到达A地.
考点:一次函数的应用
专题:
分析:(1)甲的速度=行走的路程4.8km÷所用的时间1.6;乙的速度=相遇后行走的路程4.8km÷相遇后用的时间1.2小时,把相关数值代入计算即可;
(2)利用待定系数法求一次函数解析式即可;
(3)利用(1)中所求,得出两地总路程,进而得出答案.
(2)利用待定系数法求一次函数解析式即可;
(3)利用(1)中所求,得出两地总路程,进而得出答案.
解答:解:(1)甲的速度=4.8km÷1.6=3(km/h);
乙的速度=4.8km÷(2.8-1.6)=4(km/h).
(2)设l1=kx+b,将(1.6,4,8),(2.8,0)代入得出:
,
解得:
,
∴l1=-4x+11.2,
设l2=ax,将(1.6,4.8)代入得出:
4.8=1.6a,
解得:x=3,
∴l2=3x;
(3)由l1=-4x+11.2,当x=0时,l=11.2km,
11.2÷4=2.3(小时),
答:乙需2.3小时到达A地.
乙的速度=4.8km÷(2.8-1.6)=4(km/h).
(2)设l1=kx+b,将(1.6,4,8),(2.8,0)代入得出:
|
解得:
|
∴l1=-4x+11.2,
设l2=ax,将(1.6,4.8)代入得出:
4.8=1.6a,
解得:x=3,
∴l2=3x;
(3)由l1=-4x+11.2,当x=0时,l=11.2km,
11.2÷4=2.3(小时),
答:乙需2.3小时到达A地.
点评:此题主要考查了一次函数应用以及函数图象的运用;得到每个人走的路程以及相应的时间是解决本题的易错点.

练习册系列答案
相关题目

 如图,已知∠1=∠2,∠B=∠C.
如图,已知∠1=∠2,∠B=∠C.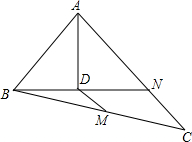 如图,在△ABC中,∠BAC=90°,AB=6,AC=8,N是AC上的点,且AN=AB,连接BN,作AD⊥BN于D,点M是BC上的动点,则当BM=
如图,在△ABC中,∠BAC=90°,AB=6,AC=8,N是AC上的点,且AN=AB,连接BN,作AD⊥BN于D,点M是BC上的动点,则当BM=