题目内容
 如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:
如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:①AE=BF;②AE⊥BF;③AO=OE;④∠CEA=∠DFB;⑤S△AOB=S四边形DEOF.
其中正确的结论有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
考点:正方形的性质,全等三角形的判定与性质
专题:
分析:根据正方形的性质得AB=AD=DC,∠BAD=∠D=90°,则由CE=DF易得AF=DE,根据“SAS”可判断△ABF≌△DAE,所以AE=BF;
根据全等的性质得∠ABF=∠EAD,∠AFB=∠DEA,利用∠EAD+∠EAB=90°得到∠ABF+∠EAB=90°,则AE⊥BF;
连结BE,BE>BC,BA≠BE,而BO⊥AE,根据垂直平分线的性质得到OA≠OE;
最后根据△ABF≌△DAE得S△ABF=S△DAE,则S△ABF-S△AOF=S△DAE-S△AOF,即S△AOB=S四边形DEOF.
根据全等的性质得∠ABF=∠EAD,∠AFB=∠DEA,利用∠EAD+∠EAB=90°得到∠ABF+∠EAB=90°,则AE⊥BF;
连结BE,BE>BC,BA≠BE,而BO⊥AE,根据垂直平分线的性质得到OA≠OE;
最后根据△ABF≌△DAE得S△ABF=S△DAE,则S△ABF-S△AOF=S△DAE-S△AOF,即S△AOB=S四边形DEOF.
解答: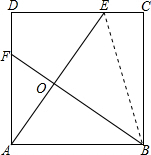 解:∵四边形ABCD为正方形,
解:∵四边形ABCD为正方形,
∴AB=AD=DC,∠BAD=∠D=90°,
而CE=DF,
∴AF=DE,
在△ABF和△DAE中
,
∴△ABF≌△DAE(SAS),
∴AE=BF,故①正确;
∴∠ABF=∠EAD,∠AFB=∠DEA,
∴∠CEA=∠DFB,故④正确;
而∠EAD+∠EAB=90°,
∴∠ABF+∠EAB=90°,
∴∠AOB=90°,
∴AE⊥BF,故②正确;
连结BE,
∵BE>BC,
∴BA≠BE,
而BO⊥AE,
∴OA≠OE,故③错误;
∵△ABF≌△DAE,
∴S△ABF=S△DAE,
∴S△ABF-S△AOF=S△DAE-S△AOF,
∴S△AOB=S四边形DEOF,故⑤正确.
综上所述,正确的结论有4个.
故选:C.
 解:∵四边形ABCD为正方形,
解:∵四边形ABCD为正方形,∴AB=AD=DC,∠BAD=∠D=90°,
而CE=DF,
∴AF=DE,
在△ABF和△DAE中
|
∴△ABF≌△DAE(SAS),
∴AE=BF,故①正确;
∴∠ABF=∠EAD,∠AFB=∠DEA,
∴∠CEA=∠DFB,故④正确;
而∠EAD+∠EAB=90°,
∴∠ABF+∠EAB=90°,
∴∠AOB=90°,
∴AE⊥BF,故②正确;
连结BE,
∵BE>BC,
∴BA≠BE,
而BO⊥AE,
∴OA≠OE,故③错误;
∵△ABF≌△DAE,
∴S△ABF=S△DAE,
∴S△ABF-S△AOF=S△DAE-S△AOF,
∴S△AOB=S四边形DEOF,故⑤正确.
综上所述,正确的结论有4个.
故选:C.
点评:本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.也考查了正方形的性质.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
下列多项式,不能运用平方差公式分解的是( )
| A、-x2-y2 |
| B、-m2+4 |
| C、y2-1 |
| D、a2-b2 |
矩形两条对角线的夹角为60°,一条对角线与短边的和为15cm,则矩形较短边长为( )
| A、4cm | B、2cm |
| C、3cm | D、5cm |
下列说法中正确的是( )
| A、“打开电视,正在播放动画片《喜洋洋和灰太狼》”是必然事件 | ||
B、某次抽奖活动中奖的概率为
| ||
C、抛掷一个正方体骰子,点数为奇数的概率是
| ||
| D、为了了解“嫦娥三号”卫星零部件的状况,检测人员采用了普查的方式 |
 如图所示,在矩形ABCD中,AB=8,BC=6,将矩形沿AC折叠后,点D落在点E处,且CE与AB交于F,求AF的长.
如图所示,在矩形ABCD中,AB=8,BC=6,将矩形沿AC折叠后,点D落在点E处,且CE与AB交于F,求AF的长. 在梯形ABCD中,AD∥BC,且AD>BC,AB=5cm,BC=6cm,梯形的高BH=4cm,P、Q分别从A、C同时出发,P以3cm/s的速度由A向D运动,Q以1cm/s的速度由C出发向B运动,
在梯形ABCD中,AD∥BC,且AD>BC,AB=5cm,BC=6cm,梯形的高BH=4cm,P、Q分别从A、C同时出发,P以3cm/s的速度由A向D运动,Q以1cm/s的速度由C出发向B运动,