题目内容
下列式子的变形,不是因式分解的有( )
①(x+1)(x-2)=x2-x-2; ②x2-2x+1=x(x-2)+1;
③x2-9y2=(x+3y)(x-3y); ④x2y-2xy+y=(x2-2x+1)y.
①(x+1)(x-2)=x2-x-2; ②x2-2x+1=x(x-2)+1;
③x2-9y2=(x+3y)(x-3y); ④x2y-2xy+y=(x2-2x+1)y.
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:因式分解的意义
专题:
分析:把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解.
解答:解:①右边不是整式积的形式,不是因式分解;
②右边不是整式积的形式,不是因式分解;
③是因式分解;
④右边的式子还有可以分解的多项式,不是因式分解;
综上可得不是因式分解的是:①②④,共3个.
故选C.
②右边不是整式积的形式,不是因式分解;
③是因式分解;
④右边的式子还有可以分解的多项式,不是因式分解;
综上可得不是因式分解的是:①②④,共3个.
故选C.
点评:本题考查了因式分解的知识,解答本题的关键是掌握因式分解的定义.

练习册系列答案
相关题目
如图是回收、绿色包装、节水、低碳四个标志,其中是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
已知实数a,b,c满足a+b+c=0,abc<0,那么
+
+
的值( )
| 2 |
| a |
| 2 |
| b |
| 2 |
| c |
| A、是正数 | B、是零 |
| C、是负数 | D、可正可负 |
下列各式由左边到右边的变形中,是分解因式的为( )
| A、a(x+y)=ax+ay |
| B、(m+1)(m-1)-(1-m)=m(m-1) |
| C、x2-16+3x=(x+4)(x-4)+3x |
| D、10x2-5x=5x(2x-1) |
下列说法中正确的个数是( )
①
的平方根是±3;②立方根等于本身的数是±1;③
=±1;④-
是5的平方根的相反数.
①
| 81 |
| 1 |
| 5 |
| A、1个 | B、2个 |
| C、3 个 | D、4个 |
7的平方根是( )
A、
| |||
B、±
| |||
C、
| |||
D、
|
 已知∠CAD=∠ADE,∠BAF=∠CDG+15°,∠BCH=120°,求∠BAF的度数.
已知∠CAD=∠ADE,∠BAF=∠CDG+15°,∠BCH=120°,求∠BAF的度数.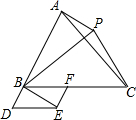 如图,点D是的边AB的延长线上的一点,点F是边BC上的一个动点(不与点B重合),以BD、BF为邻边作平行四边形BDEF,又AP∥BE,且AP=BE(点P、E在直线AB的同侧).如果BD=
如图,点D是的边AB的延长线上的一点,点F是边BC上的一个动点(不与点B重合),以BD、BF为邻边作平行四边形BDEF,又AP∥BE,且AP=BE(点P、E在直线AB的同侧).如果BD=