题目内容
16．
如图，△ABC中，将△ABC绕点A顺时针旋转40°后，得到△AB′C′，且C′在边BC上，则∠AC′C的度数为（ ）| A． | 50° | B． | 60° | C． | 70° | D． | 80° |
分析 根据旋转得出∠CAC′=40°，AC=AC′，求出∠AC′C=∠C，根据三角形内角和定理求出即可．
解答 解：∵将△ABC绕点A顺时针旋转40°后，得到△AB′C′，
∴∠CAC′=40°，AC=AC′，
∴∠AC′C=∠C=$\frac{1}{2}$（180°-∠CAC′）=70°，
故选C．
点评 本题考查了旋转的性质，等腰三角形的性质，三角形内角和定理的应用，能根据旋转的性质得出∠CAC′=40°，AC=AC′是解此题的关键．
练习册系列答案
课程达标测试卷闯关100分系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
如图，△ABC≌△ADE，BC的延长线交DE于点G，若∠B=24°，∠CAB=54°，∠DAC=16°，则∠DGB=70°．
7．
如图，已知AD∥BC，∠B=25°，DB平分∠ADE，则∠DEC等于（ ）
如图，已知AD∥BC，∠B=25°，DB平分∠ADE，则∠DEC等于（ ）| A． | 25° | B． | 50° | C． | 75° | D． | 100° |
11．
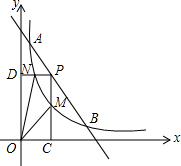如图，一次函数与反比例函数的图象交于A（1，12）和B（6，2）两点．点P是线段AB上一动点（不与点A和B重合），过P点分别作x、y轴的垂线PC、PD交反比例函数图象于点M、N，则四边形PMON面积的最大值是（ ）
如图，一次函数与反比例函数的图象交于A（1，12）和B（6，2）两点．点P是线段AB上一动点（不与点A和B重合），过P点分别作x、y轴的垂线PC、PD交反比例函数图象于点M、N，则四边形PMON面积的最大值是（ ）| A． | $\frac{25}{2}$ | B． | $\frac{25}{3}$ | C． | 6 | D． | 12 |
如图，矩形ABCD中，AB=2，BC=4，P为矩形边上的一个动点，运动路线是A→B→C→D→A，设P点经过的路程为x，以A，P，B为顶点的三角形面积为y，则选项图象能大致反映y与x的函数关系的是（ ）
5．下列图形中，既是轴对称图形，又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
