题目内容
5.三名初三学生坐在仅有的三个座位上,起身后重新就坐,恰好有两名同学没有坐回原座位的概率为( )| A. | )$\frac{1}{9}$ | B. | )$\frac{1}{6}$ | C. | )$\frac{1}{4}$ | D. | )$\frac{1}{2}$ |
分析 画树状图为(用A、B、C表示三位同学,用a、b、c表示他们原来的座位)展示所有6种等可能的结果数,再找出恰好有两名同学没有坐回原座位的结果数,然后根据概率公式求解.
解答 解:画树状图为:(用A、B、C表示三位同学,用a、b、c表示他们原来的座位)
共有6种等可能的结果数,其中恰好有两名同学没有坐回原座位的结果数为3,
所以恰好有两名同学没有坐回原座位的概率=$\frac{3}{6}$=$\frac{1}{2}$.
故选D.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案
相关题目
17.某微生物的直径为0.000 005 035m,用科学记数法表示该数为( )
| A. | 5.035×10-6 | B. | 50.35×10-5 | C. | 5.035×106 | D. | 5.035×10-5 |
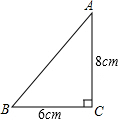 如图,一张三角形纸片ABC,∠C=90°,AC=8cm,BC=6cm.现将纸片折叠:使点A与点B重合,那么折痕长等于$\frac{15}{4}$cm.
如图,一张三角形纸片ABC,∠C=90°,AC=8cm,BC=6cm.现将纸片折叠:使点A与点B重合,那么折痕长等于$\frac{15}{4}$cm.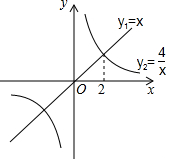 函数y1=x与y2=$\frac{4}{x}$的图象如图所示,下列关于函数y=y1+y2的结论:①函数的图象关于原点中心对称;②当x<2时,y随x的增大而减小;③当x>0时,函数的图象最低点的坐标是(2,4),其中所有正确结论的序号是①③.
函数y1=x与y2=$\frac{4}{x}$的图象如图所示,下列关于函数y=y1+y2的结论:①函数的图象关于原点中心对称;②当x<2时,y随x的增大而减小;③当x>0时,函数的图象最低点的坐标是(2,4),其中所有正确结论的序号是①③.
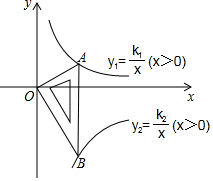 如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1=$\frac{k_1}{x}$(x>0)的图象上,顶点B在函数y2=$\frac{k_2}{x}$(x>0)的图象上,∠ABO=30°,则$\frac{k_1}{k_2}$=-$\frac{1}{3}$.
如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1=$\frac{k_1}{x}$(x>0)的图象上,顶点B在函数y2=$\frac{k_2}{x}$(x>0)的图象上,∠ABO=30°,则$\frac{k_1}{k_2}$=-$\frac{1}{3}$. 如图,⊙O是△ABC的外接圆,∠ACO=45°,则∠B的度数为45°.
如图,⊙O是△ABC的外接圆,∠ACO=45°,则∠B的度数为45°.