Question

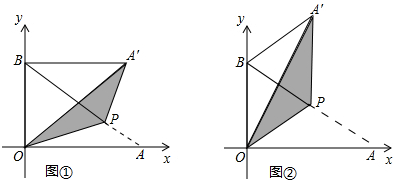
20．折纸的思考．
【操作体验】
用一张矩形纸片折等边三角形．
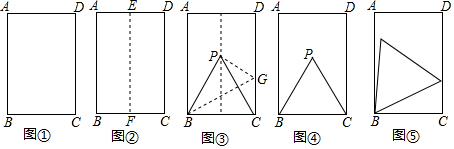
第一步，对折矩形纸片ABCD（AB＞BC）（图①），使AB与DC重合，得到折痕EF，把纸片展平（图②）．
第二步，如图③，再一次折叠纸片，使点C落在EF上的P处，并使折痕经过点B，得到折痕BG，折出PB、PC，得到△PBC．
（1）说明△PBC是等边三角形．
【数学思考】
（2）如图④，小明画出了图③的矩形ABCD和等边三角形PBC．他发现，在矩形ABCD中把△PBC经过图形变化，可以得到图⑤中的更大的等边三角形，请描述图形变化的过程．
（3）已知矩形一边长为3cm，另一边长为a cm，对于每一个确定的a的值，在矩形中都能画出最大的等边三角形，请画出不同情形的示意图，并写出对应的a的取值范围．
【问题解决】
（4）用一张正方形铁片剪一个直角边长分别为4cm和1cm的直角三角形铁片，所需正方形铁片的边长的最小值为$\frac{16}{5}$cm．

Answer 1

分析 （1）由折叠的性质和垂直平分线的性质得出PB=PC，PB=CB，得出PB=PC=CB即可；
（2）由旋转的性质和位似的性质即可得出答案；
（3）由等边三角形的性质、直角三角形的性质、勾股定理进行计算，画出图形即可；
（4）证明△AEF∽△DCE，得出$\frac{AE}{DC}=\frac{EF}{CE}$=$\frac{1}{4}$，设AE=x，则AD=CD=4x，DE=AD-AE=3x，在Rt△CDE中，由勾股定理得出方程，解方程即可．

解答 （1）证明：由折叠的性质得：EF是BC的垂直平分线，BG是PC的垂直平分线，
∴PB=PC，PB=CB，
∴PB=PC=CB，
∴△PBC是等边三角形．
（2）解：以点B为中心，在矩形ABCD中把△PBC逆时针方向旋转适当的角度，得到△P₁BC₁；
再以点B为位似中心，将△P₁BC₁放大，使点C₁的对称点C₂落在CD上，得到△P₂BC₂；
如图⑤所示；
（3）解：本题答案不唯一，举例如图⑥所示；
（4）解：如图⑦所示：
△CEF是直角三角形，∠CEF=90°，CE=4，EF=1，
∴∠AEF+∠CED=90°，
∵四边形ABCD是正方形，
∴∠A=∠D=90°，AD=CD，
∴∠DCE+∠CED=90°，
∴∠AEF=∠DCE，
∴△AEF∽△DCE，
∴$\frac{AE}{DC}=\frac{EF}{CE}$=$\frac{1}{4}$，
设AE=x，则AD=CD=4x，
∴DE=AD-AE=3x，
在Rt△CDE中，由勾股定理得：（3x）²+（4x）²=4²，
解得：x=$\frac{4}{5}$，
∴AD=4×$\frac{4}{5}$=$\frac{16}{5}$；
故答案为：$\frac{16}{5}$．

点评 本题是几何变换综合题目，考查了折叠的性质、等边三角形的判定与性质、旋转的性质、直角三角形的性质、正方形的性质、相似三角形的判定与性质、位似的性质等知识；本题综合性强，难度较大．