题目内容
18.已知方程组$\left\{\begin{array}{l}{mx+n=5}\\{my-n=1}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,则(m2-n2)的平方根是±$\sqrt{5}$.分析 把$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$代入方程组$\left\{\begin{array}{l}{mx+n=5}\\{my-n=1}\end{array}\right.$,得出$\left\{\begin{array}{l}{m+n=5}\\{m-n=1}\end{array}\right.$,可得m2-n2=(m+n)(m-n)=5,即可求出(m2-n2)的平方根.
解答 解:∵方程组$\left\{\begin{array}{l}{mx+n=5}\\{my-n=1}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,
∴$\left\{\begin{array}{l}{m+n=5}\\{m-n=1}\end{array}\right.$,
∴m2-n2=(m+n)(m-n)=5,
∴(m2-n2)的平方根是±$\sqrt{5}$.
点评 本题主要考查了二元一次方程组的解和平方根,解题的关键是正确解方程组.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
11.把100纳米(1纳米=10-6毫米)化成毫米是( )
| A. | 10-2毫米 | B. | 10-4毫米 | C. | 10-6毫米 | D. | 10-8毫米 |
6.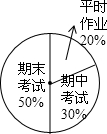 某初中一个学期的数学总平均分是按扇形图信息要求进行计算的,该校胡军同学这个学期的数学成绩如下:则胡军这个学期数学总平均分为( )
某初中一个学期的数学总平均分是按扇形图信息要求进行计算的,该校胡军同学这个学期的数学成绩如下:则胡军这个学期数学总平均分为( )
 某初中一个学期的数学总平均分是按扇形图信息要求进行计算的,该校胡军同学这个学期的数学成绩如下:则胡军这个学期数学总平均分为( )
某初中一个学期的数学总平均分是按扇形图信息要求进行计算的,该校胡军同学这个学期的数学成绩如下:则胡军这个学期数学总平均分为( ) | 胡军 | 平时作业 | 期中考试 | 期末考试 |
| 90 | 85 | 88 |
| A. | 87.5 | B. | 87.6 | C. | 87.7 | D. | 87.8 |
10.在数轴上表示不等式2x>4的解集,正确的是( )
| A. |  | B. |  | C. |  | D. |  |
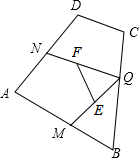 如图,四边形ABCD中,∠A=90°、AM=4、AN=3,一动点Q沿着M→B→C→D→N的路径运动(不与点M、N重合);点E、F分别为线段MQ、NQ的中点,则线段EF的长度为$\frac{5}{2}$.
如图,四边形ABCD中,∠A=90°、AM=4、AN=3,一动点Q沿着M→B→C→D→N的路径运动(不与点M、N重合);点E、F分别为线段MQ、NQ的中点,则线段EF的长度为$\frac{5}{2}$.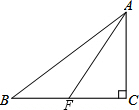 如图,在△ABC中,∠C=90°,AC=6,AB=10,F是BC边上一点.
如图,在△ABC中,∠C=90°,AC=6,AB=10,F是BC边上一点.
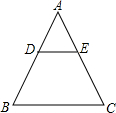 如图,在△ABC在,DE∥BC,$\frac{AD}{DB}$=$\frac{2}{3}$,S△ADE=8,则四边形BDEC的面积为42.
如图,在△ABC在,DE∥BC,$\frac{AD}{DB}$=$\frac{2}{3}$,S△ADE=8,则四边形BDEC的面积为42.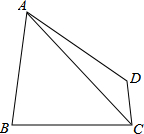 如图,在四边形ABCD中,AD=AB=BC,连接AC,且∠ACD=30°,tan∠BAC=$\frac{{2\sqrt{3}}}{3}$,CD=3,则AC=6$\sqrt{3}$.
如图,在四边形ABCD中,AD=AB=BC,连接AC,且∠ACD=30°,tan∠BAC=$\frac{{2\sqrt{3}}}{3}$,CD=3,则AC=6$\sqrt{3}$.