题目内容
9.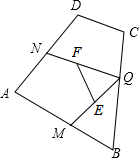 如图,四边形ABCD中,∠A=90°、AM=4、AN=3,一动点Q沿着M→B→C→D→N的路径运动(不与点M、N重合);点E、F分别为线段MQ、NQ的中点,则线段EF的长度为$\frac{5}{2}$.
如图,四边形ABCD中,∠A=90°、AM=4、AN=3,一动点Q沿着M→B→C→D→N的路径运动(不与点M、N重合);点E、F分别为线段MQ、NQ的中点,则线段EF的长度为$\frac{5}{2}$.
分析 连接MN,根据勾股定理求出MN的长,根据三角形中位线定理求出EF的长.
解答  解:连接MN,
解:连接MN,
∵∠A=90°、AM=4、AN=3,
由勾股定理得,MN=5,
∵点E、F分别为线段MQ、NQ的中点,
∴EF=$\frac{1}{2}$MN=$\frac{5}{2}$,
故答案为:$\frac{5}{2}$.
点评 本题考查的是勾股定理和三角形中位线定理的应用,正确作出辅助线、灵活运用勾股定理和三角形中位线定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2. 如图,在△ABC中,AB=AC,∠B=30°,则∠C的大小为( )
如图,在△ABC中,AB=AC,∠B=30°,则∠C的大小为( )
 如图,在△ABC中,AB=AC,∠B=30°,则∠C的大小为( )
如图,在△ABC中,AB=AC,∠B=30°,则∠C的大小为( )| A. | 15° | B. | 25° | C. | 30° | D. | 60° |
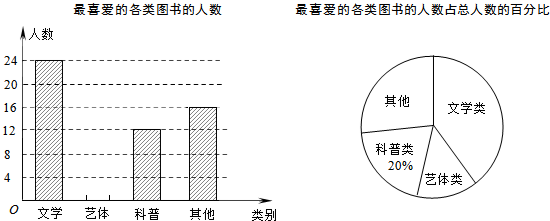
4.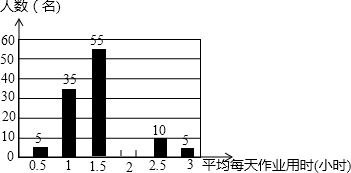 为切实减轻学生课业负担,学校教务处调查了本校学生平均每天完成作业所用时间的情况,随机调查了150名同学,下图是根据调查所得数据绘制的不完整的统计图
为切实减轻学生课业负担,学校教务处调查了本校学生平均每天完成作业所用时间的情况,随机调查了150名同学,下图是根据调查所得数据绘制的不完整的统计图
请根据图中提供信息,解答下列问题:
(1)根据题意补充条形统计图;
(2)被调查学生平均每天作业用时的众数是1.5小时,中位数是1.5小时
(3)求被调查150名学生的每天作业平均用时?假设平均每天作业用时和作业量的关系如上表,请你调查信息估计该校学生的作业量的情况?
 为切实减轻学生课业负担,学校教务处调查了本校学生平均每天完成作业所用时间的情况,随机调查了150名同学,下图是根据调查所得数据绘制的不完整的统计图
为切实减轻学生课业负担,学校教务处调查了本校学生平均每天完成作业所用时间的情况,随机调查了150名同学,下图是根据调查所得数据绘制的不完整的统计图| 平均每天作业用时t(小时) | 作业量 |
| t<1 | 较轻 |
| 1≤t≤2 | 合适 |
| t>2 | 较重 |
(1)根据题意补充条形统计图;
(2)被调查学生平均每天作业用时的众数是1.5小时,中位数是1.5小时
(3)求被调查150名学生的每天作业平均用时?假设平均每天作业用时和作业量的关系如上表,请你调查信息估计该校学生的作业量的情况?
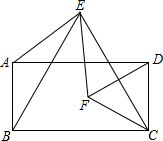 已知:如图所示,四边形ABCD是矩形,分别以BC、CD为一边作等边△EBC和等边△FCD,点E在矩形上方,点F在矩形内部,连接AE、EF.
已知:如图所示,四边形ABCD是矩形,分别以BC、CD为一边作等边△EBC和等边△FCD,点E在矩形上方,点F在矩形内部,连接AE、EF.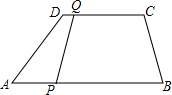 如图,在梯形ABCD中,CD∥AB,且CD=6cm,AB=9cm,P、Q分别从A、C同时出发,P以1cm/s的速度由A向B运动,Q以2cm/s的速度由C向D运动.则2或3秒时,直线QP将四边形ABCD截出一个平行四边形.
如图,在梯形ABCD中,CD∥AB,且CD=6cm,AB=9cm,P、Q分别从A、C同时出发,P以1cm/s的速度由A向B运动,Q以2cm/s的速度由C向D运动.则2或3秒时,直线QP将四边形ABCD截出一个平行四边形.