题目内容
已知一次函数y=x+b的图象与x轴,y轴交于点A、B.
(1)若将此函数图象沿x轴向右平移2个单位后经过原点,则b= ;
(2)若函数y1=x+b图象与一次函数y2=kx+4的图象关于y轴对称,求k、b的值;
(3)当b>0时,函数y1=x+b图象绕点B逆时针旋转n°(0°<n°<180°)后,对应的函数关系式为
y=-
x+b,求n的值.
(1)若将此函数图象沿x轴向右平移2个单位后经过原点,则b=
(2)若函数y1=x+b图象与一次函数y2=kx+4的图象关于y轴对称,求k、b的值;
(3)当b>0时,函数y1=x+b图象绕点B逆时针旋转n°(0°<n°<180°)后,对应的函数关系式为
y=-
| 3 |
考点:一次函数图象与几何变换
专题:
分析:(1)先根据平移的规律求出y=x+b的图象沿x轴向右平移2个单位后的解析式,再将原点的坐标代入即可求解;
(2)先求出y2=kx+4图象与y轴交点,则此交点在函数y=x+b图象上,求出b=4.再求出y1=x+4与x轴的交点坐标为(-4,0),则y2=kx-4的图象经过点(4,0),即可求出k=-1;
(3)先求出y1=x+b图象与y轴的交点B,与x轴的交点A的坐标,得出AO=BO=b(b>0),则∠ABO=45°,然后在直角△AOC中利用正切函数的定义求出∠ACB=60°,再根据三角形内角和定理即可求出n的值.
(2)先求出y2=kx+4图象与y轴交点,则此交点在函数y=x+b图象上,求出b=4.再求出y1=x+4与x轴的交点坐标为(-4,0),则y2=kx-4的图象经过点(4,0),即可求出k=-1;
(3)先求出y1=x+b图象与y轴的交点B,与x轴的交点A的坐标,得出AO=BO=b(b>0),则∠ABO=45°,然后在直角△AOC中利用正切函数的定义求出∠ACB=60°,再根据三角形内角和定理即可求出n的值.
解答:解:(1)将y=x+b的图象沿x轴向右平移2个单位后得到y=x-2+b,
由题意,得0=0-2+b,
解得b=2.
故答案为2;
(2)∵当x=0时,y=4,
∴y2=kx+4图象与y轴交于点(0,4).
∵(0,4)关于y轴对称点就是本身,
∴(0,4)在函数y=x+b图象上.
∴b=4.
∴一次函数y1=x+4,它与x轴的交点坐标为(-4,0).
∵y2=kx-4的图象与y1=x+4的图象关于y轴对称,
∴y2=kx-4的图象经过点(4,0),则0=4k+4,
∴k=-1;
(3)∵当x=0时,y1=b,
∴y1=x+b图象与y轴交于点B(0,b).
∵当y1=0时,x=-b,
∴y1=x+b图象与x轴交于点A(-b,0).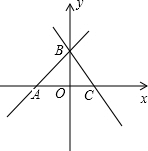
如图,∵AO=BO=b(b>0),∴∠ABO=45°.
∵当y3=0时,x=
,
∴y3=-
x+b图象与x轴交于点C(
,0).
如图,∵CO=
,
∴tan∠ACB=
=
,
∴∠ACB=60°.
∴n°=180°-∠ACB-∠BAC=75°.
即n的值为75.
由题意,得0=0-2+b,
解得b=2.
故答案为2;
(2)∵当x=0时,y=4,
∴y2=kx+4图象与y轴交于点(0,4).
∵(0,4)关于y轴对称点就是本身,
∴(0,4)在函数y=x+b图象上.
∴b=4.
∴一次函数y1=x+4,它与x轴的交点坐标为(-4,0).
∵y2=kx-4的图象与y1=x+4的图象关于y轴对称,
∴y2=kx-4的图象经过点(4,0),则0=4k+4,
∴k=-1;
(3)∵当x=0时,y1=b,
∴y1=x+b图象与y轴交于点B(0,b).
∵当y1=0时,x=-b,
∴y1=x+b图象与x轴交于点A(-b,0).

如图,∵AO=BO=b(b>0),∴∠ABO=45°.
∵当y3=0时,x=
-
| ||
| 3 |
∴y3=-
| 3 |
| ||
| 3 |
如图,∵CO=
| ||
| 3 |
∴tan∠ACB=
| b | ||||
|
| 3 |
∴∠ACB=60°.
∴n°=180°-∠ACB-∠BAC=75°.
即n的值为75.
点评:本题考查了一次函数图象与几何变换,一次函数图象上点的坐标特征,正切函数的定义,三角形内角和定理,综合性较强,有一定难度.

练习册系列答案
相关题目
下列命题正确的是( )
A、3x-7>0的解集为x>
| ||
B、
| ||
| C、9的平方根是3 | ||
D、8.5<
|
已知△ABC的三边长分别为a,b,c,如果
+|b-4|+a2-10a+25=0,那么△ABC是( )
| c-3 |
| A、以a为斜边的直角三角形 |
| B、以b为斜边的直角三角形 |
| C、以c为斜边的直角三角形 |
| D、形状不能确定 |
 如图,在?ABCD中,点E,F在BD上,BE=DF求证:AE=CF.
如图,在?ABCD中,点E,F在BD上,BE=DF求证:AE=CF.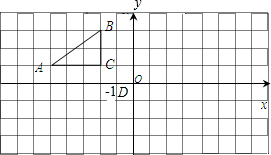 如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-5,1),点B的坐标为(-2,3),点C的坐标为(-2,1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-5,1),点B的坐标为(-2,3),点C的坐标为(-2,1).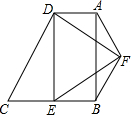 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,∠C=60°,BC=2AD=2
如图,在四边形ABCD中,AD∥BC,∠ABC=90°,∠C=60°,BC=2AD=2