题目内容
6．
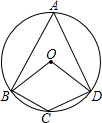如图，四边形ABCD是⊙O的内接四边形，且OB∥DC，OD∥BC，则∠BOD=120°．
分析 先判断四边形OBCD为平行四边形，则根据平行四边形的性质得∠C=∠BOD，再根据圆内接四边形的性质得∠C+∠A=180°，根据圆周角定理得∠A=$\frac{1}{2}$∠BOD，所以∠BOD+$\frac{1}{2}$∠BOD=180°，然后解方程即可．
解答 解：∵OB∥DC，OD∥BC，
∴四边形OBCD为平行四边形，
∴∠C=∠BOD，
∵∠C+∠A=180°，
而∠A=$\frac{1}{2}$∠BOD，
∴∠BOD+$\frac{1}{2}$∠BOD=180°，
∴∠BOD=120°．
故答案为120°．
点评 本题考查了圆内接四边形的性质：圆内接四边形的对角互补．也考查了平行四边形的性质．
练习册系列答案
相关题目
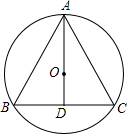⊙0外接等腰△ABC，AB=AC，连AO并延长BC与D，BC=12，cosB=$\frac{3}{5}$，求：半径长．