题目内容
如图,在△ABC中,D,E分别是AB,AC边上的中点,连接DE,那么△ADE与△ABC的面积之比是( )
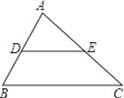

A.1:16 B.1:9 C.1:4 D.1:2
C【考点】相似三角形的判定与性质;三角形中位线定理.
【专题】计算题.
【分析】由于D,E分别是AB,AC边上的中点,利用三角形中位线定理可知DE∥BC,
 =
=
 ,再利用平行线分线段成比例定理的推论易证△ADE∽△ABC,再利用相似三角形面积比等于相似比的平方可求两个三角形面积比.
,再利用平行线分线段成比例定理的推论易证△ADE∽△ABC,再利用相似三角形面积比等于相似比的平方可求两个三角形面积比.
【解答】解:∵D,E分别是AB,AC边上的中点,
∴DE∥BC,
 =
=
 ,
,
∴△ADE∽△ABC,
∴S△ADE:S△ABC=(
 )2=
)2=
 .
.
故选C.
【点评】本题考查了相似三角形的判定和性质、平行线分线段成比例定理的推论、三角形中位线定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
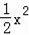
 +bx+c的图象经过A(2,0)、B(0,﹣6)两点.
+bx+c的图象经过A(2,0)、B(0,﹣6)两点.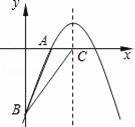

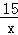 的图象经过点C.
的图象经过点C.




 (x>0) C.y=
(x>0) C.y= =1,则 ( )
=1,则 ( ) 2 C. x≠
2 C. x≠ D. x为任意有理数
D. x为任意有理数