Question

【题目】若二次函数图象的顶点在一次函数的图象上，则称为的中雅函数，如：是的中雅函数．

(1)判断二次函数是否为一次函数的中雅函数，并说明理由；

(2)若关于的一次函数的中雅函数与轴两个交点间的距离为，求直线与坐标轴所围三角形的面积；

(3)已知关于的一次函数的中雅函数为，与平行的直线交中雅函数的图象于、两点，若轴上有且仅有一个点，使得，求的值．

Answer 1

【答案】（1）见解析；（2）；（3）

【解析】

（1）先求出顶点坐标，代入，判断是否是上的点即可求解．

（2）先求出的顶点坐标，根据是一次函数的中雅函数，列出等式，将m用n表示出来，设与轴两个交点分别为x1，x2

两点间距离，求出n，即可求出m，得出直线解析式，即可求出直线与坐标轴所围三角形的面积．

（3）求出的顶点坐标，根据是一次函数的中雅函数，得出，已知直线与平行，即可得出，再求出与交点A、B坐标，AB长，AB中点C的纵坐标，轴上有且仅有一个点，使得，则说明以AB为直径的圆与x轴相切，则点C纵坐标等于以AB为直径的圆的半径，列出等式即可求出k．

（1）∵

，

∴的顶点坐标为(1,-5)

当x=1时，≠-5

∴二次函数不是一次函数的中雅函数

故答案为：二次函数不是一次函数的中雅函数，理由见解析

（2）的顶点坐标为：

，

∵是一次函数的中雅函数

∴

解得

∵与轴两个交点分别为x1，x2

∵，

解得n=±6

当n=6时，m=

当n=-6时，m=

或

一次函数中，

令x=0，y=-3

令y=0，x=9

与坐标轴所围三角形的面积为

一次函数中

令x=0，y=3

令y=0，x=-9

与坐标轴所围三角形的面积为

∴直线与坐标轴所围三角形的面积为

故答案为：

（3）的顶点坐标为：

，

∵是一次函数的中雅函数

∴

∴

∵直线与平行

∴n=m=3k

∴

设与交于A、B两点

令

解得x=3或x=-1

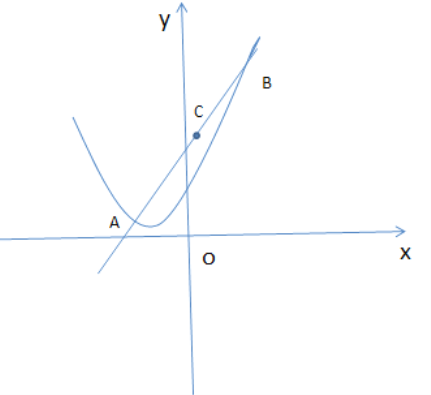
∴A(-1,4k)，B(3,16k)

∴AB=

取AB的中点C，则C点纵坐标为6k+4k=10k

若轴上有且仅有一个点，使得，则说明以AB为直径的圆与x轴相切

则点C纵坐标等于以AB为直径的圆的半径

即10k=

解得k=±

又∵k＞0

∴k=

故答案为：