Question

【题目】已知点是反比例函数图象上的动点，轴，轴，分别交反比例函数的图象于点、，交坐标轴于、，且，连接.现有以下四个结论：①；②在点运动过程中，的面积始终不变；③连接，则；④不存在点，使得.其中正确的结论的序号是__________．

Answer 1

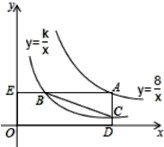
【答案】①②③

【解析】

①由反比例函数图象上点的坐标特征用函数a的代数式表示出来b，并找出点C坐标，根据AC=3CD，即可得出关于k的一元一次方程，解方程即可得出结论；

②根据①得出A、C的坐标，由AB∥x轴找出B点的坐标，由此即可得出AB、AC的长度，利用三角形的面积公式即可得出结论；

③已知B(,)，C(a,)，D(a,0)，E(0,)四点坐标，B、C、D、E四点坐标，经过B、C两点的直线斜率k1=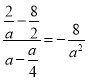，经过D、E两点的直线斜率k2=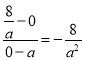，得出，即

④先假设，得到对应边成比例，列出关于a的等式，看a是否有解，即可求解．

①∵A(a,b)，且A在反比例函数的图象上，
∴

∵AC∥y轴，且C在反比例函数的图象上，
∴C(a,)

又∵AC=3CD，

∴AD=4CD，即

∴k=2．

故①正确

②由①可知：A(a,)，C(a,)

∵AB∥x轴，

∴B点的纵坐标为，

∵点B在反比例函数的函数图象上，
∴，解得：x=，
∴点B(,)，
∴AB=a=，AC==

∴S=AB×AC=××=

∴在点A运动过程中，△ABC面积不变，始终等于

故②正确

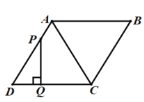
③连接DE，如图所示

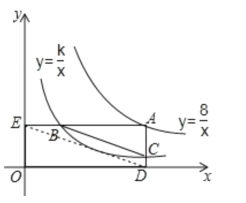
∵B(,)，C(a,)

∴经过B、C两点的直线斜率k1=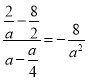

∵轴，轴

∴D(a,0)，E(0,)

∴经过D、E两点的直线斜率k2=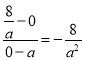

∴，即

故③正确

④假设

∴

∴

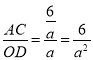
解得

∴当时，

故④错误

故答案为：①②③