题目内容
 如图,已知双曲线
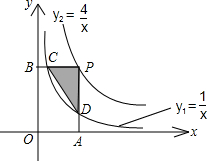
如图,已知双曲线 (k≠0)与直线y=x交于A、C两点,AB⊥x轴于点B,若S△ABC=4,则k=________.
(k≠0)与直线y=x交于A、C两点,AB⊥x轴于点B,若S△ABC=4,则k=________.
4
分析:过C作CD⊥X轴于D,设A的坐标是(a,b),根据双曲线的性质得到C的坐标是(-a,-b),根据三角形的面积公式推出 ×a×b+
×a×b+ ×a×b=4,代入即可求出k.
×a×b=4,代入即可求出k.
解答: 解:过C作CD⊥X轴于D,
解:过C作CD⊥X轴于D,
设A的坐标是(a,b),则根据双曲线的两个分支关于原点对称,则C的坐标是(-a,-b),
则ab=k,OB=a,AB=b,CD=b,
∵S△ABC=S△AOB+S△COB=4,
∴ ×a×b+
×a×b+ ×a×b=4,
×a×b=4,
即 k+
k+ k=4,
k=4,
k=4,
故答案为:4.
点评:本题主要考查对三角形的面积,反比例函数的性质,一次函数与反比例函数的交点问题等知识点的理解和掌握,能推出 k+
k+ k=4是解此题的关键.
k=4是解此题的关键.
分析:过C作CD⊥X轴于D,设A的坐标是(a,b),根据双曲线的性质得到C的坐标是(-a,-b),根据三角形的面积公式推出
 ×a×b+
×a×b+ ×a×b=4,代入即可求出k.
×a×b=4,代入即可求出k.解答:
 解:过C作CD⊥X轴于D,
解:过C作CD⊥X轴于D,设A的坐标是(a,b),则根据双曲线的两个分支关于原点对称,则C的坐标是(-a,-b),
则ab=k,OB=a,AB=b,CD=b,
∵S△ABC=S△AOB+S△COB=4,
∴
 ×a×b+
×a×b+ ×a×b=4,
×a×b=4,即
 k+
k+ k=4,
k=4,k=4,
故答案为:4.
点评:本题主要考查对三角形的面积,反比例函数的性质,一次函数与反比例函数的交点问题等知识点的理解和掌握,能推出
 k+
k+ k=4是解此题的关键.
k=4是解此题的关键. 
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 如图,已知双曲线
如图,已知双曲线 (2012•济南)如图,已知双曲线y=
(2012•济南)如图,已知双曲线y= (2013•徐州模拟)如图,已知双曲线y=
(2013•徐州模拟)如图,已知双曲线y= 如图,已知双曲线
如图,已知双曲线 如图,已知双曲线
如图,已知双曲线