题目内容
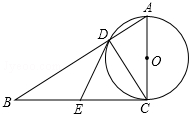 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,点E是边BC的中点.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,点E是边BC的中点.(1)求证:DE与⊙O相切;
(2)当以点O、D、E、C为顶点的四边形是平行四边形时,⊙O的半径为1,求△ABC的面积.
考点:切线的判定,平行四边形的性质
专题:
分析:(1)运用垂径定理、直角三角形的性质证明∠ODE=90°即可解决问题;
(2)根据平行四边形的对边相等的性质和三角形的面积公式进行解答.
(2)根据平行四边形的对边相等的性质和三角形的面积公式进行解答.
解答: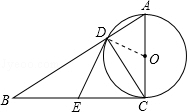 (1)证明:连接OD.
(1)证明:连接OD.
∵AC是直径,
∴∠ADC=90°,
∴∠CDB=90°,
又∵EB=EC
∴DE为直角△DCB斜边的中线,
∴DE=CE=
.
∴∠DCE=∠CDE,
∵OC=OD,
∴∠OCD=∠ODC,
∴∠ODC+∠CDE=∠OCD+∠DCE=∠ACB=90°,
∴∠ODE=90°
∴DE是⊙O的切线.
(2)∵四边形OCED是平行四边形,
∴OC=DE,
∴BC=2DE=2OC=2×1=2.AC=2OC=2,
∴S△ABC=
BC•AC=
×2×2=2.
 (1)证明:连接OD.
(1)证明:连接OD.∵AC是直径,
∴∠ADC=90°,
∴∠CDB=90°,
又∵EB=EC
∴DE为直角△DCB斜边的中线,
∴DE=CE=
| 1 |
| 2 |
∴∠DCE=∠CDE,
∵OC=OD,
∴∠OCD=∠ODC,
∴∠ODC+∠CDE=∠OCD+∠DCE=∠ACB=90°,
∴∠ODE=90°
∴DE是⊙O的切线.
(2)∵四边形OCED是平行四边形,
∴OC=DE,
∴BC=2DE=2OC=2×1=2.AC=2OC=2,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了切线的判定与性质、圆周角定理的推论、直角三形的性质等几何知识点的考查;该命题以圆为载体,以切线的判定为考查的核心构造而成;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
已知⊙O中,圆心角∠AOB=100°,则圆周角∠ACB等于( )
| A、50° |
| B、100°或50° |
| C、130°或50° |
| D、130° |
在比例尺为1:m的某市地图上,规划出长a厘米,宽b厘米的矩形工业园区,该园区的实际面积是( )米2.
A、
| ||
B、
| ||
C、
| ||
D、
|
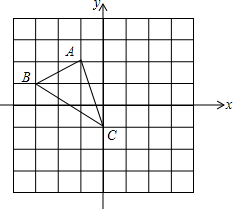 如图所示,已知△ABC,点A、B、C的坐标分别为(-1,2)、(-3,1)、(0,-1)
如图所示,已知△ABC,点A、B、C的坐标分别为(-1,2)、(-3,1)、(0,-1)